Tips on how to examine a loud quantum processor to a classical laptop – Google Analysis Weblog
A full-scale error-corrected quantum laptop will be capable to resolve some issues which are unattainable for classical computer systems, however constructing such a tool is a large endeavor. We’re happy with the milestones that now we have achieved towards a totally error-corrected quantum laptop, however that large-scale laptop continues to be some variety of years away. In the meantime, we’re utilizing our present noisy quantum processors as versatile platforms for quantum experiments.
In distinction to an error-corrected quantum laptop, experiments in noisy quantum processors are at present restricted to some thousand quantum operations or gates, earlier than noise degrades the quantum state. In 2019 we applied a selected computational job known as random circuit sampling on our quantum processor and showed for the primary time that it outperformed state-of-the-art classical supercomputing.
Though they haven’t but reached beyond-classical capabilities, now we have additionally used our processors to watch novel bodily phenomena, reminiscent of time crystals and Majorana edge modes, and have made new experimental discoveries, reminiscent of sturdy bound states of interacting photons and the noise-resilience of Majorana edge modes of Floquet evolutions.
We anticipate that even on this intermediate, noisy regime, we are going to discover purposes for the quantum processors through which helpful quantum experiments may be carried out a lot quicker than may be calculated on classical supercomputers — we name these “computational purposes” of the quantum processors. Nobody has but demonstrated such a beyond-classical computational utility. In order we intention to realize this milestone, the query is: What’s one of the best ways to match a quantum experiment run on such a quantum processor to the computational price of a classical utility?
We already know how you can examine an error-corrected quantum algorithm to a classical algorithm. In that case, the sector of computational complexity tells us that we will examine their respective computational prices — that’s, the variety of operations required to perform the duty. However with our present experimental quantum processors, the state of affairs just isn’t so properly outlined.
In “Effective quantum volume, fidelity and computational cost of noisy quantum processing experiments”, we offer a framework for measuring the computational price of a quantum experiment, introducing the experiment’s “efficient quantum quantity”, which is the variety of quantum operations or gates that contribute to a measurement final result. We apply this framework to judge the computational price of three latest experiments: our random circuit sampling experiment, our experiment measuring quantities known as “out of time order correlators” (OTOCs), and a recent experiment on a Floquet evolution associated to the Ising model. We’re notably enthusiastic about OTOCs as a result of they supply a direct approach to experimentally measure the efficient quantum quantity of a circuit (a sequence of quantum gates or operations), which is itself a computationally tough job for a classical laptop to estimate exactly. OTOCs are additionally vital in nuclear magnetic resonance and electron spin resonance spectroscopy. Subsequently, we consider that OTOC experiments are a promising candidate for a first-ever computational utility of quantum processors.
 |
| Plot of computational price and influence of some latest quantum experiments. Whereas some (e.g., QC-QMC 2022) have had excessive influence and others (e.g., RCS 2023) have had excessive computational price, none have but been each helpful and arduous sufficient to be thought-about a “computational utility.” We hypothesize that our future OTOC experiment might be the primary to cross this threshold. Different experiments plotted are referenced within the textual content. |
Random circuit sampling: Evaluating the computational price of a loud circuit
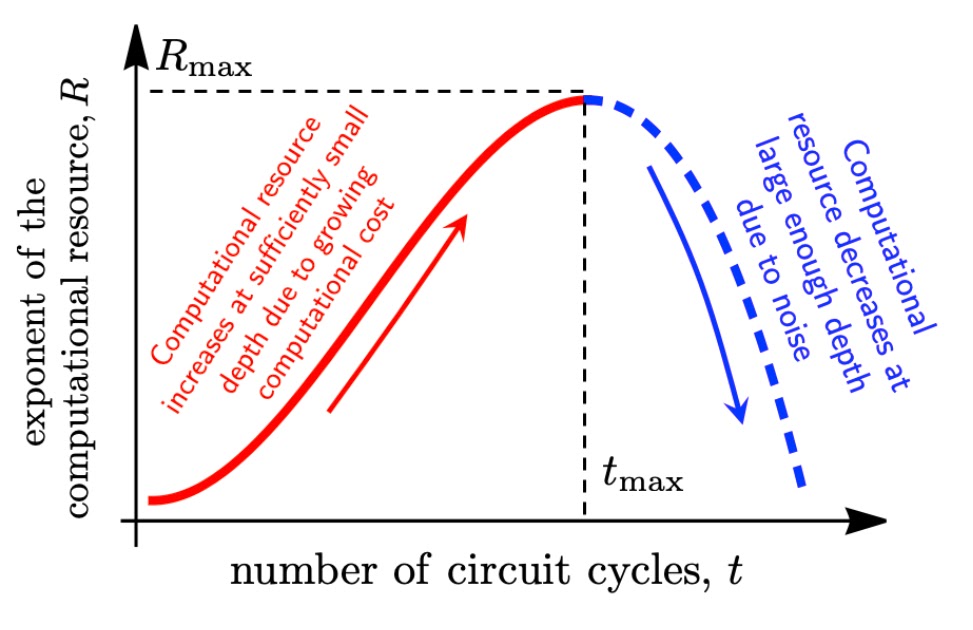
On the subject of working a quantum circuit on a loud quantum processor, there are two competing concerns. On one hand, we intention to do one thing that’s tough to realize classically. The computational price — the variety of operations required to perform the duty on a classical laptop — will depend on the quantum circuit’s efficient quantum quantity: the bigger the quantity, the upper the computational price, and the extra a quantum processor can outperform a classical one.
However however, on a loud processor, every quantum gate can introduce an error to the calculation. The extra operations, the upper the error, and the decrease the constancy of the quantum circuit in measuring a amount of curiosity. Beneath this consideration, we would want less complicated circuits with a smaller efficient quantity, however these are simply simulated by classical computer systems. The stability of those competing concerns, which we wish to maximize, is known as the “computational useful resource”, proven beneath.
 |
| Graph of the tradeoff between quantum quantity and noise in a quantum circuit, captured in a amount known as the “computational useful resource.” For a loud quantum circuit, it will initially enhance with the computational price, however ultimately, noise will overrun the circuit and trigger it to lower. |
We are able to see how these competing concerns play out in a easy “hello world” program for quantum processors, often known as random circuit sampling (RCS), which was the primary demonstration of a quantum processor outperforming a classical laptop. Any error in any gate is more likely to make this experiment fail. Inevitably, it is a arduous experiment to realize with important constancy, and thus it additionally serves as a benchmark of system constancy. However it additionally corresponds to the best identified computational price achievable by a quantum processor. We not too long ago reported the most powerful RCS experiment carried out to this point, with a low measured experimental constancy of 1.7×10-3, and a excessive theoretical computational price of ~1023. These quantum circuits had 700 two-qubit gates. We estimate that this experiment would take ~47 years to simulate on the earth’s largest supercomputer. Whereas this checks one of many two bins wanted for a computational utility — it outperforms a classical supercomputer — it’s not a very helpful utility per se.
OTOCs and Floquet evolution: The efficient quantum quantity of a neighborhood observable
There are numerous open questions in quantum many-body physics which are classically intractable, so working a few of these experiments on our quantum processor has nice potential. We sometimes consider these experiments a bit in another way than we do the RCS experiment. Quite than measuring the quantum state of all qubits on the finish of the experiment, we’re often involved with extra particular, native bodily observables. As a result of not each operation within the circuit essentially impacts the observable, a neighborhood observable’s efficient quantum quantity is perhaps smaller than that of the complete circuit wanted to run the experiment.
We are able to perceive this by making use of the idea of a lightweight cone from relativity, which determines which occasions in space-time may be causally related: some occasions can not presumably affect each other as a result of info takes time to propagate between them. We are saying that two such occasions are outdoors their respective gentle cones. In a quantum experiment, we exchange the sunshine cone with one thing known as a “butterfly cone,” the place the expansion of the cone is set by the butterfly velocity — the velocity with which info spreads all through the system. (This velocity is characterised by measuring OTOCs, mentioned later.) The efficient quantum quantity of a neighborhood observable is basically the quantity of the butterfly cone, together with solely the quantum operations which are causally related to the observable. So, the quicker info spreads in a system, the bigger the efficient quantity and due to this fact the tougher it’s to simulate classically.
 |
| An outline of the efficient quantity Veff of the gates contributing to the native observable B. A associated amount known as the efficient space Aeff is represented by the cross-section of the aircraft and the cone. The perimeter of the bottom corresponds to the entrance of knowledge journey that strikes with the butterfly velocity vB. |
We apply this framework to a latest experiment implementing a so-called Floquet Ising mannequin, a bodily mannequin associated to the time crystal and Majorana experiments. From the information of this experiment, one can immediately estimate an efficient constancy of 0.37 for the most important circuits. With the measured gate error charge of ~1%, this offers an estimated efficient quantity of ~100. That is a lot smaller than the sunshine cone, which included two thousand gates on 127 qubits. So, the butterfly velocity of this experiment is kind of small. Certainly, we argue that the efficient quantity covers solely ~28 qubits, not 127, utilizing numerical simulations that get hold of a bigger precision than the experiment. This small efficient quantity has additionally been corroborated with the OTOC method. Though this was a deep circuit, the estimated computational price is 5×1011, virtually one trillion occasions lower than the latest RCS experiment. Correspondingly, this experiment may be simulated in lower than a second per knowledge level on a single A100 GPU. So, whereas that is actually a helpful utility, it doesn’t fulfill the second requirement of a computational utility: considerably outperforming a classical simulation.
Info scrambling experiments with OTOCs are a promising avenue for a computational utility. OTOCs can inform us vital bodily details about a system, such because the butterfly velocity, which is essential for exactly measuring the efficient quantum quantity of a circuit. OTOC experiments with quick entangling gates supply a possible path for a primary beyond-classical demonstration of a computational utility with a quantum processor. Certainly, in our experiment from 2021 we achieved an efficient constancy of Feff ~ 0.06 with an experimental signal-to-noise ratio of ~1, similar to an efficient quantity of ~250 gates and a computational price of 2×1012.
Whereas these early OTOC experiments usually are not sufficiently complicated to outperform classical simulations, there’s a deep bodily motive why OTOC experiments are good candidates for the primary demonstration of a computational utility. A lot of the fascinating quantum phenomena accessible to near-term quantum processors which are arduous to simulate classically correspond to a quantum circuit exploring many, many quantum power ranges. Such evolutions are sometimes chaotic and normal time-order correlators (TOC) decay in a short time to a purely random common on this regime. There isn’t a experimental sign left. This doesn’t occur for OTOC measurements, which permits us to develop complexity at will, solely restricted by the error per gate. We anticipate {that a} discount of the error charge by half would double the computational price, pushing this experiment to the beyond-classical regime.
Conclusion
Utilizing the efficient quantum quantity framework now we have developed, now we have decided the computational price of our RCS and OTOC experiments, in addition to a latest Floquet evolution experiment. Whereas none of those meet the necessities but for a computational utility, we anticipate that with improved error charges, an OTOC experiment would be the first beyond-classical, helpful utility of a quantum processor.
