Past computerized differentiation – Google AI Weblog

Derivatives play a central position in optimization and machine studying. By domestically approximating a training loss, derivatives information an optimizer towards decrease values of the loss. Computerized differentiation frameworks reminiscent of TensorFlow, PyTorch, and JAX are a necessary a part of fashionable machine studying, making it possible to make use of gradient-based optimizers to coach very advanced fashions.

However are derivatives all we’d like? By themselves, derivatives solely inform us how a perform behaves on an infinitesimal scale. To make use of derivatives successfully, we frequently have to know greater than that. For instance, to decide on a learning rate for gradient descent, we have to know one thing about how the loss perform behaves over a small however finite window. A finite-scale analogue of computerized differentiation, if it existed, may assist us make such decisions extra successfully and thereby pace up coaching.

In our new paper “Automatically Bounding The Taylor Remainder Series: Tighter Bounds and New Applications“, we current an algorithm known as AutoBound that computes polynomial higher and decrease bounds on a given perform, that are legitimate over a user-specified interval. We then start to discover AutoBound’s functions. Notably, we current a meta-optimizer known as SafeRate that makes use of the higher bounds computed by AutoBound to derive studying charges which are assured to monotonically cut back a given loss perform, with out the necessity for time-consuming hyperparameter tuning. We’re additionally making AutoBound obtainable as an open-source library.

The AutoBound algorithm

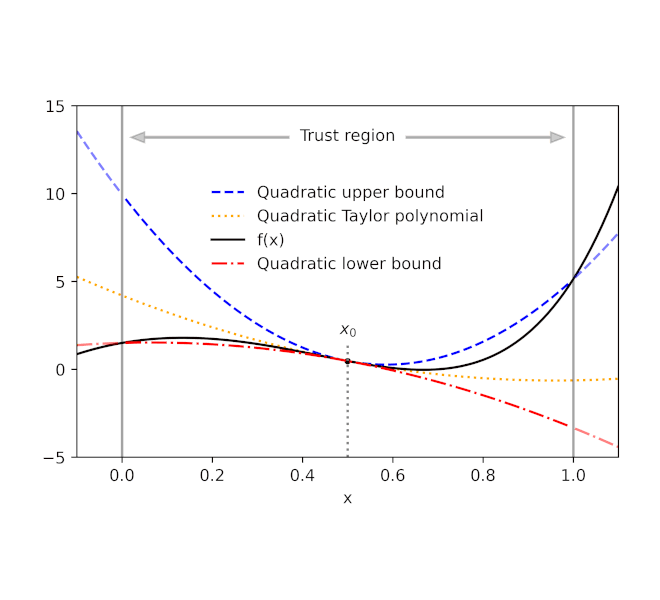
Given a perform f and a reference level x0, AutoBound computes polynomial higher and decrease bounds on f that maintain over a user-specified interval known as a belief area. Like Taylor polynomials, the bounding polynomials are equal to f at x0. The bounds develop into tighter because the belief area shrinks, and strategy the corresponding Taylor polynomial because the belief area width approaches zero.

Routinely-derived quadratic higher and decrease bounds on a one-dimensional perform f, centered at x0=0.5. The higher and decrease bounds are legitimate over a user-specified belief area, and develop into tighter because the belief area shrinks.

Like computerized differentiation, AutoBound may be utilized to any perform that may be carried out utilizing normal mathematical operations. In actual fact, AutoBound is a generalization of Taylor mode automatic differentiation, and is equal to it within the particular case the place the belief area has a width of zero.

To derive the AutoBound algorithm, there have been two most important challenges we needed to handle:

1. We needed to derive polynomial higher and decrease bounds for varied elementary features, given an arbitrary reference level and arbitrary belief area.
2. We needed to give you an analogue of the chain rule for combining these bounds.

Bounds for elementary features

For quite a lot of commonly-used features, we derive optimum polynomial higher and decrease bounds in closed type. On this context, “optimum” means the bounds are as tight as potential, amongst all polynomials the place solely the maximum-degree coefficient differs from the Taylor sequence. Our concept applies to elementary features, reminiscent of exp and log, and customary neural community activation features, reminiscent of ReLU and Swish. It builds upon and generalizes earlier work that utilized solely to quadratic bounds, and just for an unbounded belief area.

Optimum quadratic higher and decrease bounds on the exponential perform, centered at x0=0.5 and legitimate over the interval [0, 2].

A brand new chain rule

To compute higher and decrease bounds for arbitrary features, we derived a generalization of the chain rule that operates on polynomial bounds. For instance the thought, suppose now we have a perform that may be written as

and suppose we have already got polynomial higher and decrease bounds on g and h. How can we compute bounds on f?

The important thing seems to be representing the higher and decrease bounds for a given perform as a single polynomial whose highest-degree coefficient is an interval slightly than a scalar. We will then plug the sure for h into the sure for g, and convert the end result again to a polynomial of the identical type utilizing interval arithmetic. Beneath appropriate assumptions concerning the belief area over which the sure on g holds, it may be proven that this process yields the specified sure on f.

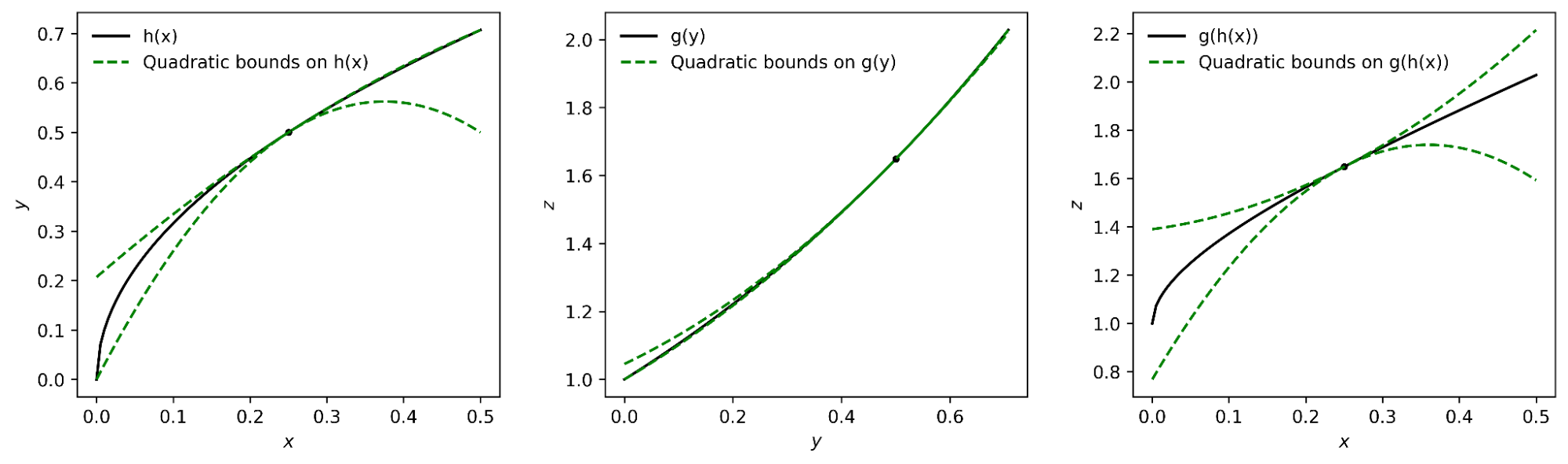The interval polynomial chain rule utilized to the features h(x) = sqrt(x) and g(y) = exp(y), with x0=0.25 and belief area [0, 0.5].

Our chain rule applies to one-dimensional features, but additionally to multivariate features, reminiscent of matrix multiplications and convolutions.

Propagating bounds

Utilizing our new chain rule, AutoBound propagates interval polynomial bounds by a computation graph from the inputs to the outputs, analogous to forward-mode automatic differentiation.

Ahead propagation of interval polynomial bounds for the perform f(x) = exp(sqrt(x)). We first compute (trivial) bounds on x, then use the chain rule to compute bounds on sqrt(x) and exp(sqrt(x)).

To compute bounds on a perform f(x), AutoBound requires reminiscence proportional to the dimension of x. For that reason, sensible functions apply AutoBound to features with a small variety of inputs. Nonetheless, as we are going to see, this doesn’t forestall us from utilizing AutoBound for neural community optimization.

Routinely deriving optimizers, and different functions

What can we do with AutoBound that we could not do with computerized differentiation alone?

Amongst different issues, AutoBound can be utilized to robotically derive problem-specific, hyperparameter-free optimizers that converge from any start line. These optimizers iteratively cut back a loss by first utilizing AutoBound to compute an higher sure on the loss that’s tight on the present level, after which minimizing the higher sure to acquire the following level.

Minimizing a one-dimensional logistic regression loss utilizing quadratic higher bounds derived robotically by AutoBound.

Optimizers that use higher bounds on this manner are known as majorization-minimization (MM) optimizers. Utilized to one-dimensional logistic regression, AutoBound rederives an MM optimizer first published in 2009. Utilized to extra advanced issues, AutoBound derives novel MM optimizers that might be troublesome to derive by hand.

We will use an identical concept to take an present optimizer reminiscent of Adam and convert it to a hyperparameter-free optimizer that’s assured to monotonically cut back the loss (within the full-batch setting). The ensuing optimizer makes use of the identical replace path as the unique optimizer, however modifies the educational fee by minimizing a one-dimensional quadratic higher sure derived by AutoBound. We seek advice from the ensuing meta-optimizer as SafeRate.

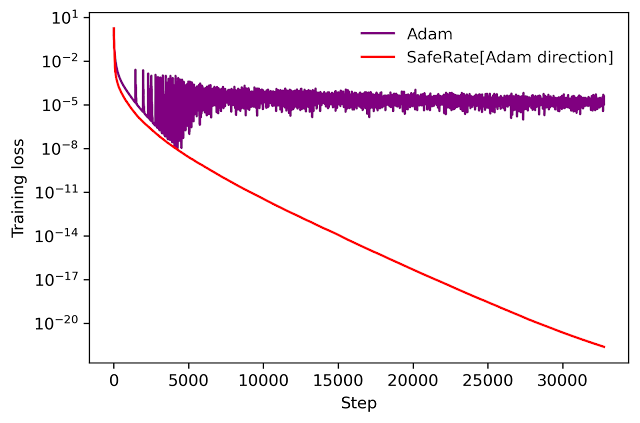Efficiency of SafeRate when used to coach a single-hidden-layer neural community on a subset of the MNIST dataset, within the full-batch setting.

Utilizing SafeRate, we are able to create extra strong variants of present optimizers, at the price of a single extra ahead cross that will increase the wall time for every step by a small issue (about 2x within the instance above).

Along with the functions simply mentioned, AutoBound can be utilized for verified numerical integration and to robotically show sharper variations of Jensen’s inequality, a basic mathematical inequality used steadily in statistics and different fields.

Enchancment over classical bounds

Bounding the Taylor remainder term robotically isn’t a brand new concept. A classical method produces diploma okay polynomial bounds on a perform f which are legitimate over a belief area [a, b] by first computing an expression for the okayth spinoff of f (utilizing computerized differentiation), then evaluating this expression over [a,b] utilizing interval arithmetic.

Whereas elegant, this strategy has some inherent limitations that may result in very free bounds, as illustrated by the dotted blue strains within the determine under.

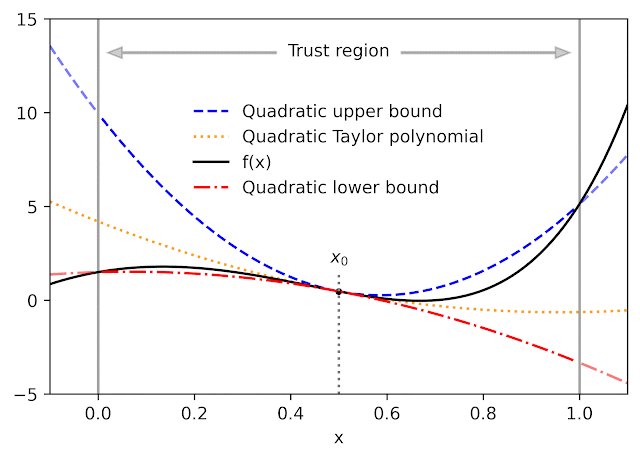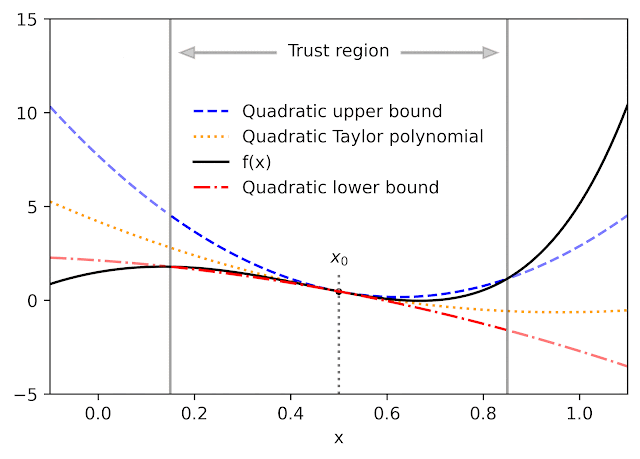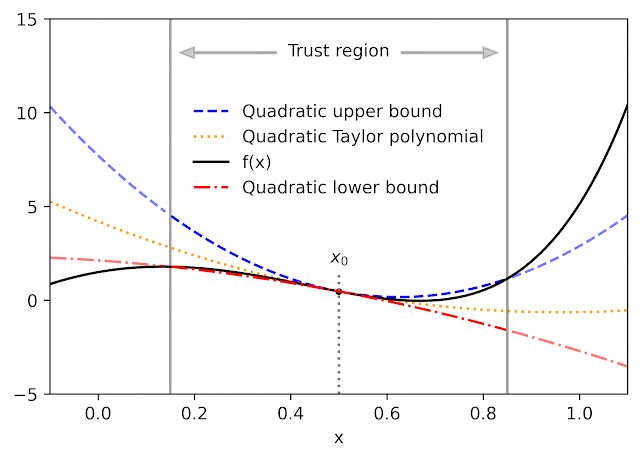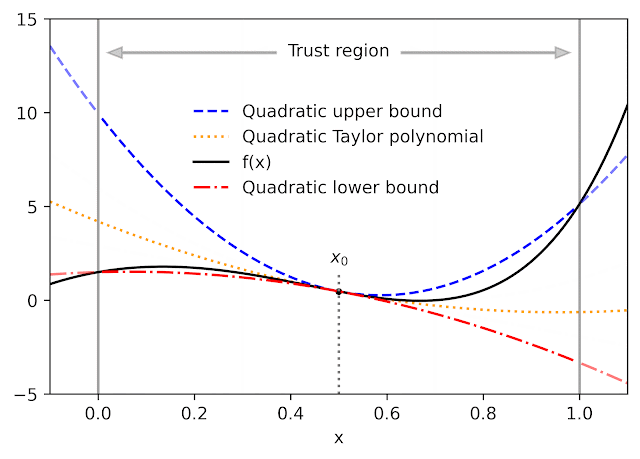
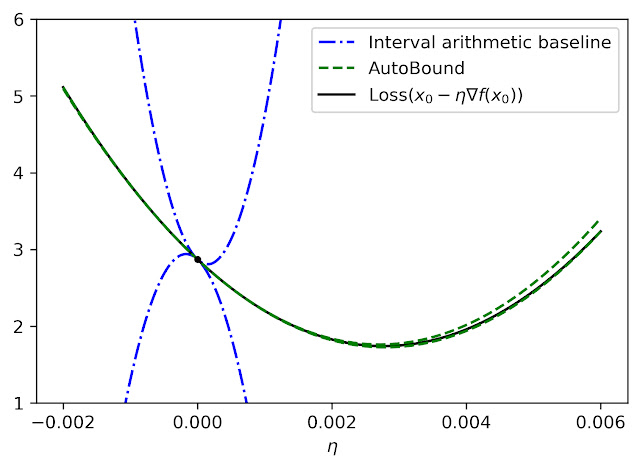Quadratic higher and decrease bounds on the lack of a multi-layer perceptron with two hidden layers, as a perform of the preliminary studying fee. The bounds derived by AutoBound are a lot tighter than these obtained utilizing interval arithmetic analysis of the second spinoff.

Trying ahead

Taylor polynomials have been in use for over 300 years, and are omnipresent in numerical optimization and scientific computing. Nonetheless, Taylor polynomials have vital limitations, which might restrict the capabilities of algorithms constructed on high of them. Our work is a part of a rising literature that acknowledges these limitations and seeks to develop a brand new basis upon which extra strong algorithms may be constructed.

Our experiments thus far have solely scratched the floor of what’s potential utilizing AutoBound, and we consider it has many functions now we have not found. To encourage the analysis neighborhood to discover such potentialities, now we have made AutoBound obtainable as an open-source library constructed on high of JAX. To get began, go to our GitHub repo.

Acknowledgements

This publish is predicated on joint work with Josh Dillon. We thank Alex Alemi and Sergey Ioffe for priceless suggestions on an earlier draft of the publish.