How does temperature impression subsequent token prediction in LLMs? | by Ankur Manikandan | Could, 2024
Introduction
Massive Language Fashions (LLMs) are versatile generative fashions suited to a big selection of duties. They will produce constant, repeatable outputs or generate artistic content material by inserting unlikely phrases collectively. The “temperature” setting permits customers to fine-tune the mannequin’s output, controlling the diploma of predictability.
Let’s take a hypothetical instance to grasp the impression of temperature on the subsequent token prediction.
We requested an LLM to finish the sentence, “This can be a fantastic _____.” Let’s assume the potential candidate tokens are:
| token | logit |
|------------|-------|
| day | 40 |
| house | 4 |
| furnishings | 2 |
| expertise | 35 |
| downside | 25 |
| problem | 15 |
The logits are handed by means of a softmax perform in order that the sum of the values is the same as one. Primarily, the softmax perform generates chance estimates for every token.
Let’s calculate the chance estimates in Python.
import numpy as np
import seaborn as sns
import pandas as pd
import matplotlib.pyplot as plt
from ipywidgets import interactive, FloatSliderdef softmax(logits):
exps = np.exp(logits)
return exps / np.sum(exps)
knowledge = {
"tokens": ["day", "space", "furniture", "experience", "problem", "challenge"],
"logits": [5, 2.2, 2.0, 4.5, 3.0, 2.7]
}
df = pd.DataFrame(knowledge)
df['probabilities'] = softmax(df['logits'].values)
df
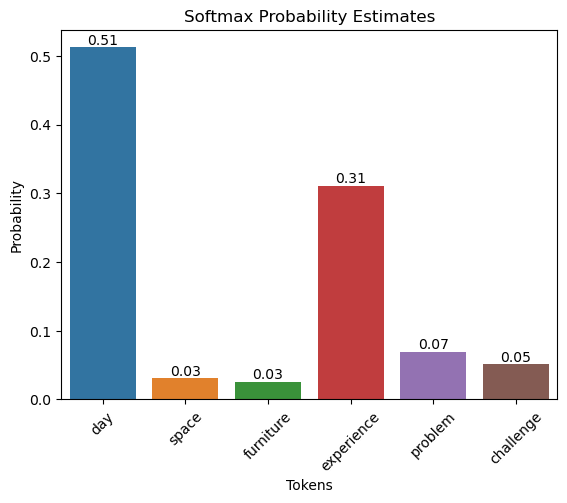
| No. | tokens | logits | chances |
|-----|------------|--------|---------------|
| 0 | day | 5.0 | 0.512106 |
| 1 | house | 2.2 | 0.031141 |
| 2 | furnishings | 2.0 | 0.025496 |
| 3 | expertise | 4.5 | 0.310608 |
| 4 | downside | 3.0 | 0.069306 |
| 5 | problem | 2.7 | 0.051343 |
ax = sns.barplot(x="tokens", y="chances", knowledge=df)
ax.set_title('Softmax Likelihood Estimates')
ax.set_ylabel('Likelihood')
ax.set_xlabel('Tokens')
plt.xticks(rotation=45)
for bar in ax.patches:
ax.textual content(bar.get_x() + bar.get_width() / 2, bar.get_height(), f'{bar.get_height():.2f}',
ha='middle', va='backside', fontsize=10, rotation=0)
plt.present()
The softmax perform with temperature is outlined as follows:
the place (T) is the temperature, (x_i) is the (i)-th element of the enter vector (logits), and (n) is the variety of parts within the vector.
def softmax_with_temperature(logits, temperature):
if temperature <= 0:
temperature = 1e-10 # Stop division by zero or unfavorable temperatures
scaled_logits = logits / temperature
exps = np.exp(scaled_logits - np.max(scaled_logits)) # Numerical stability enchancment
return exps / np.sum(exps)def plot_interactive_softmax(temperature):
chances = softmax_with_temperature(df['logits'], temperature)
plt.determine(figsize=(10, 5))
bars = plt.bar(df['tokens'], chances, shade='blue')
plt.ylim(0, 1)
plt.title(f'Softmax Possibilities at Temperature = {temperature:.2f}')
plt.ylabel('Likelihood')
plt.xlabel('Tokens')
# Add textual content annotations
for bar, chance in zip(bars, chances):
yval = bar.get_height()
plt.textual content(bar.get_x() + bar.get_width()/2, yval, f"{chance:.2f}", ha='middle', va='backside', fontsize=10)
plt.present()
interactive_plot = interactive(plot_interactive_softmax, temperature=FloatSlider(worth=1, min=0, max=2, step=0.01, description='Temperature'))
interactive_plot
At T = 1,
At a temperature of 1, the chance values are the identical as these derived from the usual softmax perform.
At T > 1,
Elevating the temperature inflates the possibilities of the much less seemingly tokens, thereby broadening the vary of potential candidates (or variety) for the mannequin’s subsequent token prediction.
At T < 1,
Reducing the temperature, however, makes the chance of the most certainly token method 1.0, boosting the mannequin’s confidence. Reducing the temperature successfully eliminates the uncertainty inside the mannequin.
Conclusion
LLMs leverage the temperature parameter to supply flexibility of their predictions. The mannequin behaves predictably at a temperature of 1, carefully following the unique softmax distribution. Rising the temperature introduces larger variety, amplifying much less seemingly tokens. Conversely, reducing the temperature makes the predictions extra targeted, rising the mannequin’s confidence in essentially the most possible token by lowering uncertainty. This adaptability permits customers to tailor LLM outputs to a big selection of duties, placing a steadiness between artistic exploration and deterministic output.