Don’t over-think about ‘outliers’, use a student-t distribution as a substitute | by Daniel Manrique-Castano | Mar, 2024
A Student’s t-distribution is nothing greater than a Gaussian distribution with heavier tails. In different phrases, we will say that the Gaussian distribution is a particular case of the Scholar’s t-distribution. The Gaussian distribution is outlined by the imply (μ) and the usual deviation (σ). The Scholar t distribution, however, provides a further parameter, the levels of freedom (df), which controls the “thickness” of the distribution. This parameter assigns larger likelihood to occasions farther from the imply. This characteristic is especially helpful for small pattern sizes, equivalent to in biomedicine, the place the idea of normality is questionable. Be aware that because the levels of freedom enhance, the Scholar t-distribution approaches the Gaussian distribution. We are able to visualize this utilizing density plots:
# Load essential libraries
library(ggplot2)# Set seed for reproducibility
set.seed(123)
# Outline the distributions
x <- seq(-4, 4, size.out = 200)
y_gaussian <- dnorm(x)
y_t3 <- dt(x, df = 3)
y_t10 <- dt(x, df = 10)
y_t30 <- dt(x, df = 30)
# Create an information body for plotting
df <- information.body(x, y_gaussian, y_t3, y_t10, y_t30)
# Plot the distributions
ggplot(df, aes(x)) +
geom_line(aes(y = y_gaussian, coloration = "Gaussian")) +
geom_line(aes(y = y_t3, coloration = "t, df=3")) +
geom_line(aes(y = y_t10, coloration = "t, df=10")) +
geom_line(aes(y = y_t30, coloration = "t, df=30")) +
labs(title = "Comparability of Gaussian and Scholar t-Distributions",
x = "Worth",
y = "Density") +
scale_color_manual(values = c("Gaussian" = "blue", "t, df=3" = "purple", "t, df=10" = "inexperienced", "t, df=30" = "purple")) +
theme_classic()
Be aware in Figure 1 that the hill across the imply will get smaller because the levels of freedom lower because of the likelihood mass going to the tails, that are thicker. This property is what provides the Scholar’s t-distribution a lowered sensitivity to outliers. For extra particulars on this matter, you may examine this weblog.
We load the required libraries:
library(ggplot2)
library(brms)
library(ggdist)
library(easystats)
library(dplyr)
library(tibble)
library(ghibli)
So, let’s skip information simulations and get severe. We’ll work with actual information I’ve acquired from mice performing the rotarod take a look at.
First, we load the dataset into the environment and set the corresponding issue ranges. The dataset comprises IDs for the animals, a groping variable (Genotype), an indicator for 2 totally different days on which the take a look at was carried out (day), and totally different trials for a similar day. For this text, we mannequin solely one of many trials (Trial3). We are going to save the opposite trials for a future article on modeling variation.
As the information dealing with implies, our modeling technique shall be based mostly on Genotype and Day as categorical predictors of the distribution of Trial3.
In biomedical science, categorical predictors, or grouping components, are extra frequent than steady predictors. Scientists on this area wish to divide their samples into teams or situations and apply totally different remedies.
information <- learn.csv("Knowledge/Rotarod.csv")
information$Day <- issue(information$Day, ranges = c("1", "2"))
information$Genotype <- issue(information$Genotype, ranges = c("WT", "KO"))
head(information)
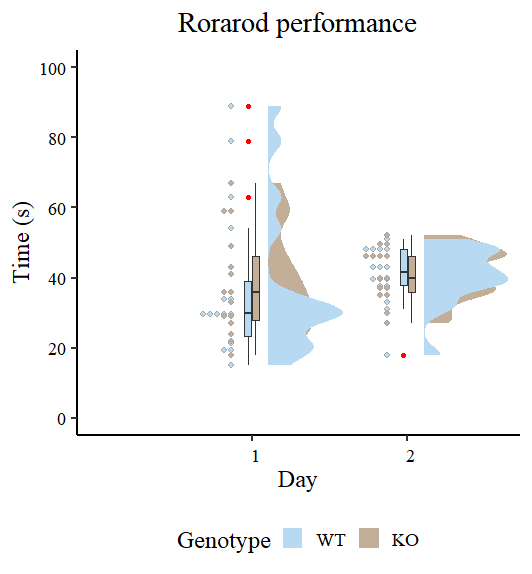
Let’s have an preliminary view of the information utilizing Raincloud plots as proven by Guilherme A. Franchi, PhD in this nice weblog put up.
edv <- ggplot(information, aes(x = Day, y = Trial3, fill=Genotype)) +
scale_fill_ghibli_d("SpiritedMedium", route = -1) +
geom_boxplot(width = 0.1,
outlier.coloration = "purple") +
xlab('Day') +
ylab('Time (s)') +
ggtitle("Rorarod efficiency") +
theme_classic(base_size=18, base_family="serif")+
theme(textual content = element_text(dimension=18),
axis.textual content.x = element_text(angle=0, hjust=.1, vjust = 0.5, coloration = "black"),
axis.textual content.y = element_text(coloration = "black"),
plot.title = element_text(hjust = 0.5),
plot.subtitle = element_text(hjust = 0.5),
legend.place="backside")+
scale_y_continuous(breaks = seq(0, 100, by=20),
limits=c(0,100)) +
# Line beneath provides dot plots from {ggdist} bundle
stat_dots(facet = "left",
justification = 1.12,
binwidth = 1.9) +
# Line beneath provides half-violin from {ggdist} bundle
stat_halfeye(modify = .5,
width = .6,
justification = -.2,
.width = 0,
point_colour = NA)
edv
Figure 2 appears to be like totally different from the unique by Guilherme A. Franchi, PhD as a result of we’re plotting two components as a substitute of 1. Nevertheless, the character of the plot is identical. Take note of the purple dots, these are those that may be thought-about excessive observations that tilt the measures of central tendency (particularly the imply) towards one route. We additionally observe that the variances are totally different, so modeling additionally sigma can provide higher estimates. Our activity now could be to mannequin the output utilizing the brms bundle.




