The world’s first braiding of non-Abelian anyons – Google AI Weblog

Think about you’re proven two an identical objects after which requested to shut your eyes. While you open your eyes, you see the identical two objects in the identical place. How will you decide if they’ve been swapped forwards and backwards? Instinct and the legal guidelines of quantum mechanics agree: If the objects are actually an identical, there is no such thing as a solution to inform.

Whereas this seems like widespread sense, it solely applies to our acquainted three-dimensional world. Researchers have predicted that for a particular kind of particle, known as an anyon, that’s restricted to maneuver solely in a two-dimensional (2D) airplane, quantum mechanics permits for one thing fairly totally different. Anyons are indistinguishable from each other and a few, non-Abelian anyons, have a particular property that causes observable variations within the shared quantum state below change, making it doable to inform once they have been exchanged, regardless of being absolutely indistinguishable from each other. Whereas researchers have managed to detect their relations, Abelian anyons, whose change below change is extra refined and inconceivable to straight detect, realizing “non-Abelian change conduct” has confirmed tougher as a result of challenges with each management and detection.

In “Non-Abelian braiding of graph vertices in a superconducting processor”, printed in Nature, we report the remark of this non-Abelian change conduct for the primary time. Non-Abelian anyons may open a brand new avenue for quantum computation, wherein quantum operations are achieved by swapping particles round each other like strings are swapped round each other to create braids. Realizing this new change conduct on our superconducting quantum processor could possibly be an alternate path to so-called topological quantum computation, which advantages from being sturdy in opposition to environmental noise.

Trade statistics and non-Abelian anyons

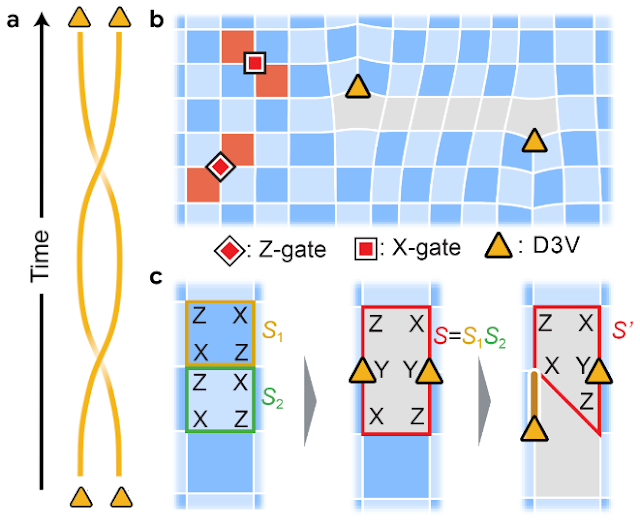
So as to perceive how this unusual non-Abelian conduct can happen, it’s useful to contemplate an analogy with the braiding of two strings. Take two an identical strings and lay them parallel subsequent to at least one one other. Swap their ends to kind a double-helix form. The strings are an identical, however as a result of they wrap round each other when the ends are exchanged, it is vitally clear when the 2 ends are swapped.

The change of non-Abelian anyons will be visualized in an analogous manner, the place the strings are produced from extending the particles’ positions into the time dimension to kind “world-lines.” Think about plotting two particles’ areas vs. time. If the particles keep put, the plot would merely be two parallel strains, representing their fixed areas. But when we change the areas of the particles, the world strains wrap round each other. Trade them a second time, and also you’ve made a knot.

Whereas a bit tough to visualise, knots in 4 dimensions (three spatial plus one time dimension) can at all times simply be undone. They’re trivial — like a shoelace, merely pull one finish and it unravels. However when the particles are restricted to 2 spatial dimensions, the knots are in three complete dimensions and — as we all know from our on a regular basis 3D lives — can’t at all times be simply untied. The braiding of the non-Abelian anyons’ world strains can be utilized as quantum computing operations to rework the state of the particles.

A key facet of non-Abelian anyons is “degeneracy”: the complete state of a number of separated anyons will not be utterly specified by native data, permitting the identical anyon configuration to characterize superpositions of a number of quantum states. Winding non-Abelian anyons about one another can change the encoded state.

Easy methods to make a non-Abelian anyon

So how can we understand non-Abelian braiding with one among Google’s quantum processors? We begin with the acquainted floor code, which we lately used to realize a milestone in quantum error correction, the place qubits are organized on the vertices of a checkerboard sample. Every colour sq. of the checkerboard represents one among two doable joint measurements that may be made from the qubits on the 4 corners of the sq.. These so-called “stabilizer measurements” can return a price of both + or – 1. The latter is known as a plaquette violation, and will be created and moved diagonally — similar to bishops in chess — by making use of single-qubit X- and Z-gates. Lately, we confirmed that these bishop-like plaquette violations are Abelian anyons. In distinction to non-Abelian anyons, the state of Abelian anyons modifications solely subtly when they’re swapped — so subtly that it’s inconceivable to straight detect. Whereas Abelian anyons are attention-grabbing, they don’t maintain the identical promise for topological quantum computing that non-Abelian anyons do.

To supply non-Abelian anyons, we have to management the degeneracy (i.e., the variety of wavefunctions that causes all stabilizer measurements to be +1). Since a stabilizer measurement returns two doable values, every stabilizer cuts the degeneracy of the system in half, and with sufficiently many stabilizers, just one wave operate satisfies the criterion. Therefore, a easy solution to improve the degeneracy is to merge two stabilizers collectively. Within the technique of doing so, we take away one edge within the stabilizer grid, giving rise to 2 factors the place solely three edges intersect. These factors, known as “degree-3 vertices” (D3Vs), are predicted to be non-Abelian anyons.

So as to braid the D3Vs, we’ve got to maneuver them, which means that we’ve got to stretch and squash the stabilizers into new shapes. We accomplish this by implementing two-qubit gates between the anyons and their neighbors (center and proper panels proven beneath).

Non-Abelian anyons in stabilizer codes. a: Instance of a knot made by braiding two anyons’ world strains. b: Single-qubit gates can be utilized to create and transfer stabilizers with a price of –1 (pink squares). Like bishops in chess, these can solely transfer diagonally and are subsequently constrained to at least one sublattice within the common floor code. This constraint is damaged when D3Vs (yellow triangles) are launched. c: Course of to kind and transfer D3Vs (predicted to be non-Abelian anyons). We begin with the floor code, the place every sq. corresponds to a joint measurement of the 4 qubits on its corners (left panel). We take away an edge separating two neighboring squares, such that there’s now a single joint measurement of all six qubits (center panel). This creates two D3Vs, that are non-Abelian anyons. We transfer the D3Vs by making use of two-qubit gates between neighboring websites (proper panel).

Now that we’ve got a solution to create and transfer the non-Abelian anyons, we have to confirm their anyonic conduct. For this we study three traits that might be anticipated of non-Abelian anyons:

1. The “fusion rules” — What occurs when non-Abelian anyons collide with one another?
2. Trade statistics — What occurs when they’re braided round each other?
3. Topological quantum computing primitives — Can we encode qubits within the non-Abelian anyons and use braiding to carry out two-qubit entangling operations?

The fusion guidelines of non-Abelian anyons

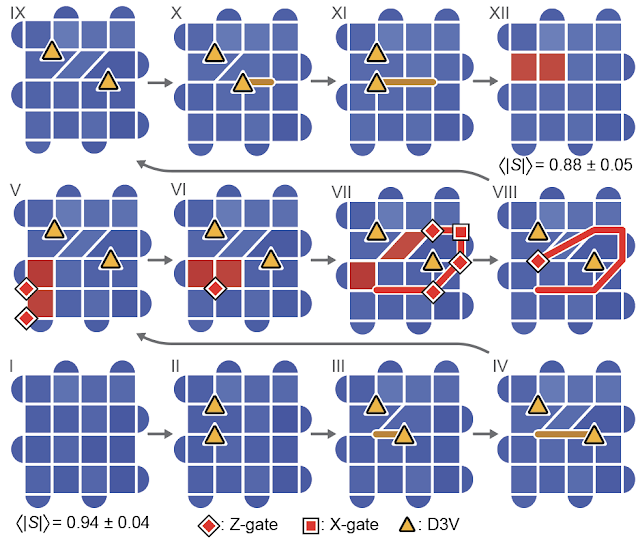
We examine fusion guidelines by learning how a pair of D3Vs work together with the bishop-like plaquette violations launched above. Specifically, we create a pair of those and produce one among them round a D3V by making use of single-qubit gates.

Whereas the principles of bishops in chess dictate that the plaquette violations can by no means meet, the dislocation within the checkerboard lattice permits them to interrupt this rule, meet its companion and annihilate with it. The plaquette violations have now disappeared! However carry the non-Abelian anyons again involved with each other, and the anyons out of the blue morph into the lacking plaquette violations. As bizarre as this conduct appears, it’s a manifestation of precisely the fusion guidelines that we anticipate these entities to obey. This establishes confidence that the D3Vs are, certainly, non-Abelian anyons.

Demonstration of anyonic fusion guidelines (beginning with panel I, within the decrease left). We kind and separate two D3Vs (yellow triangles), then kind two adjoining plaquette violations (pink squares) and cross one between the D3Vs. The D3Vs deformation of the “chessboard” modifications the bishop guidelines of the plaquette violations. Whereas they used to lie on adjoining squares, they’re now in a position to transfer alongside the identical diagonals and collide (as proven by the pink strains). Once they do collide, they annihilate each other. The D3Vs are introduced again collectively and surprisingly morph into the lacking adjoining pink plaquette violations.

Remark of non-Abelian change statistics

After establishing the fusion guidelines, we need to see the true smoking gun of non-Abelian anyons: non-Abelian change statistics. We create two pairs of non-Abelian anyons, then braid them by wrapping one from every pair round one another (proven beneath). After we fuse the 2 pairs again collectively, two pairs of plaquette violations seem. The easy act of braiding the anyons round each other modified the observables of our system. In different phrases, when you closed your eyes whereas the non-Abelian anyons had been being exchanged, you’ll nonetheless be capable of inform that they’d been exchanged when you opened your eyes. That is the hallmark of non-Abelian statistics.

Braiding non-Abelian anyons. We make two pairs of D3Vs (panel II), then carry one from every pair round one another (III-XI). When fusing the 2 pairs collectively once more in panel XII, two pairs of plaquette violations seem! Braiding the non-Abelian anyons modified the observables of the system from panel I to panel XII; a direct manifestation of non-Abelian change statistics.

Topological quantum computing

Lastly, after establishing their fusion guidelines and change statistics, we exhibit how we are able to use these particles in quantum computations. The non-Abelian anyons can be utilized to encode data, represented by logical qubits, which must be distinguished from the precise bodily qubits used within the experiment. The variety of logical qubits encoded in N D3Vs will be proven to be N/2–1, so we use N=8 D3Vs to encode three logical qubits, and carry out braiding to entangle them. By learning the ensuing state, we discover that the braiding has certainly led to the formation of the specified, well-known quantum entangled state known as the Greenberger-Horne-Zeilinger (GHZ) state.

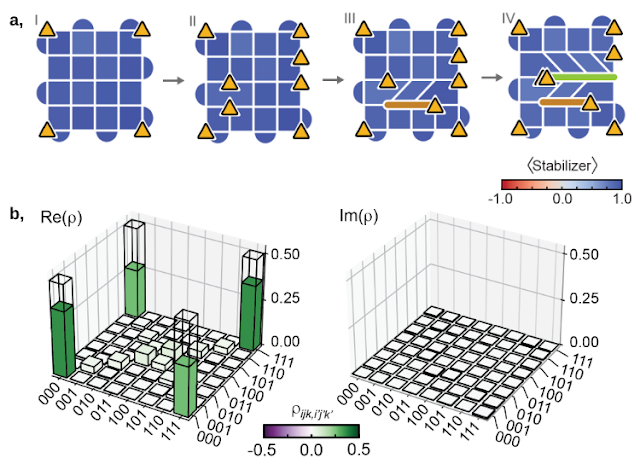Utilizing non-Abelian anyons as logical qubits. a, We braid the non-Abelian anyons to entangle three qubits encoded in eight D3Vs. b, Quantum state tomography permits for reconstructing the density matrix, which will be represented in a 3D bar plot and is discovered to be in line with the specified extremely entangled GHZ-state.

Conclusion

Our experiments present the primary remark of non-Abelian change statistics, and that braiding of the D3Vs can be utilized to carry out quantum computations. With future additions, together with error correction in the course of the braiding process, this could possibly be a significant step in direction of topological quantum computation, a long-sought technique to endow qubits with intrinsic resilience in opposition to fluctuations and noise that might in any other case trigger errors in computations.

Acknowledgements

We want to thank Katie McCormick, our Quantum Science Communicator, for serving to to jot down this weblog submit.