Differentially personal heatmaps – Google AI Weblog

Just lately, differential privacy (DP) has emerged as a mathematically strong notion of person privateness for information aggregation and machine studying (ML), with sensible deployments together with the 2022 US Census and in trade. Over the previous couple of years, we now have open-sourced libraries for privacy-preserving analytics and ML and have been constantly enhancing their capabilities. In the meantime, new algorithms have been developed by the analysis group for a number of analytic duties involving personal aggregation of knowledge.
One such necessary information aggregation methodology is the heatmap. Heatmaps are in style for visualizing aggregated information in two or extra dimensions. They’re broadly utilized in many fields together with laptop imaginative and prescient, picture processing, spatial information evaluation, bioinformatics, and extra. Defending the privateness of person information is crucial for a lot of purposes of heatmaps. For instance, heatmaps for gene microdata are based mostly on personal information from people. Equally, a heatmap of in style areas in a geographic space are based mostly on person location check-ins that must be saved personal.
Motivated by such purposes, in “Differentially Private Heatmaps” (introduced at AAAI 2023), we describe an environment friendly DP algorithm for computing heatmaps with provable ensures and consider it empirically. On the core of our DP algorithm for heatmaps is an answer to the fundamental downside of how one can privately combination sparse enter vectors (i.e., enter vectors with a small variety of non-zero coordinates) with a small error as measured by the Earth Mover’s Distance (EMD). Utilizing a hierarchical partitioning process, our algorithm views every enter vector, in addition to the output heatmap, as a likelihood distribution over quite a few gadgets equal to the dimension of the info. For the issue of sparse aggregation beneath EMD, we give an environment friendly algorithm with error asymptotically near the absolute best.
Algorithm description
Our algorithm works by privatizing the aggregated distribution (obtained by averaging over all person inputs), which is enough for computing a remaining heatmap that’s personal attributable to the post-processing property of DP. This property ensures that any transformation of the output of a DP algorithm stays differentially personal. Our foremost contribution is a brand new privatization algorithm for the aggregated distribution, which we’ll describe subsequent.
The EMD measure, which is a distance-like measure of dissimilarity between two likelihood distributions initially proposed for laptop imaginative and prescient duties, is well-suited for heatmaps because it takes the underlying metric area into consideration and considers “neighboring” bins. EMD is utilized in quite a lot of purposes together with deep learning, spatial evaluation, human mobility, picture retrieval, face recognition, visible monitoring, form matching, and extra.
To realize DP, we have to add noise to the aggregated distribution. We might additionally prefer to protect statistics at completely different scales of the grid to attenuate the EMD error. So, we create a hierarchical partitioning of the grid, add noise at every degree, after which recombine into the ultimate DP aggregated distribution. Particularly, the algorithm has the next steps:
- Quadtree building: Our hierarchical partitioning process first divides the grid into 4 cells, then divides every cell into 4 subcells; it recursively continues this course of till every cell is a single pixel. This process creates a quadtree over the subcells the place the basis represents your complete grid and every leaf represents a pixel. The algorithm then calculates the whole likelihood mass for every tree node (obtained by including up the aggregated distribution’s chances of all leaves within the subtree rooted at this node). This step is illustrated beneath.

In step one, we take the (non-private) aggregated distribution (prime left) and repeatedly divide it to create a quadtree. Then, we compute the whole likelihood mass is every cell (backside). - Noise addition: To every tree node’s mass we then add Laplace noise calibrated to the use case.
- Truncation: To assist cut back the ultimate quantity of noise in our DP aggregated distribution, the algorithm traverses the tree ranging from the basis and, at every degree, it discards all however the prime w nodes with highest (noisy) lots along with their descendants.
- Reconstruction: Lastly, the algorithm solves a linear program to recuperate the aggregated distribution. This linear program is impressed by the sparse recovery literature the place the noisy lots are seen as (noisy) measurements of the info.
Experimental outcomes
We consider the efficiency of our algorithm in two completely different domains: real-world location check-in information and picture saliency information. We contemplate as a baseline the ever present Laplace mechanism, the place we add Laplace noise to every cell, zero out any destructive cells, and produce the heatmap from this noisy combination. We additionally contemplate a “thresholding” variant of this baseline that’s extra suited to sparse information: solely maintain prime t% of the cell values (based mostly on the likelihood mass in every cell) after noising whereas zeroing out the remainder. To judge the standard of an output heatmap in comparison with the true heatmap, we use Pearson coefficient, KL-divergence, and EMD. Word that when the heatmaps are extra comparable, the primary metric will increase however the latter two lower.
The areas dataset is obtained by combining two datasets, Gowalla and Brightkite, each of which include check-ins by customers of location-based social networks. We pre-processed this dataset to think about solely check-ins within the continental US leading to a remaining dataset consisting of ~500,000 check-ins by ~20,000 customers. Contemplating the highest cells (from an preliminary partitioning of your complete area right into a 300 x 300 grid) which have check-ins from no less than 200 distinctive customers, we partition every such cell into subgrids with a decision of ∆ × ∆ and assign every check-in to one in all these subgrids.
Within the first set of experiments, we repair ∆ = 256. We take a look at the efficiency of our algorithm for various values of ε (the privacy parameter, the place smaller ε means stronger DP ensures), starting from 0.1 to 10, by operating our algorithms along with the baseline and its variants on all cells, randomly sampling a set of 200 customers in every trial, after which computing the gap metrics between the true heatmap and the DP heatmap. The typical of those metrics is introduced beneath. Our algorithm (the crimson line) performs higher than all variations of the baseline throughout all metrics, with enhancements which can be particularly vital when ε will not be too massive or small (i.e., 0.2 ≤ ε ≤ 5).
 |
| Metrics averaged over 60 runs when various ε for the placement dataset. Shaded areas point out 95% confidence interval. |
Subsequent, we research the impact of various the quantity n of customers. By fixing a single cell (with > 500 customers) and ε, we range n from 50 to 500 customers. As predicted by concept, our algorithms and the baseline carry out higher as n will increase. Nonetheless, the conduct of the thresholding variants of the baseline are much less predictable.
We additionally run one other experiment the place we repair a single cell and ε, and range the decision ∆ from 64 to 256. In settlement with concept, our algorithm’s efficiency stays practically fixed for your complete vary of ∆. Nonetheless, the baseline suffers throughout all metrics as ∆ will increase whereas the thresholding variants often enhance as ∆ will increase.
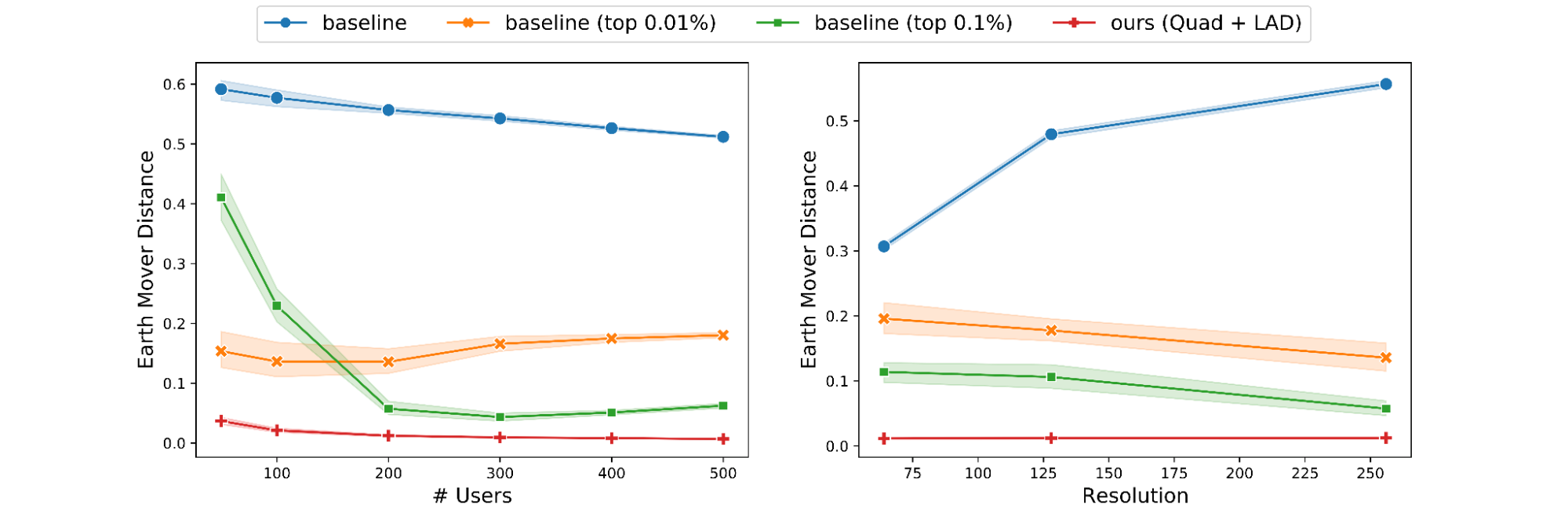 |
| Impact of the variety of customers and grid decision on EMD. |
We additionally experiment on the Salicon image saliency dataset (SALICON). This dataset is a set of saliency annotations on the Microsoft Common Objects in Context picture database. We downsized the photographs to a hard and fast decision of 320 × 240 and every [user, image] pair consists of a sequence of coordinates within the picture the place the person regarded. We repeat the experiments described beforehand on 38 randomly sampled photographs (with ≥ 50 customers every) from SALICON. As we are able to see from the examples beneath, the heatmap obtained by our algorithm could be very near the bottom fact.
Further experimental outcomes, together with these on different datasets, metrics, privateness parameters and DP fashions, might be discovered within the paper.
Conclusion
We introduced a privatization algorithm for sparse distribution aggregation beneath the EMD metric, which in flip yields an algorithm for producing privacy-preserving heatmaps. Our algorithm extends naturally to distributed fashions that may implement the Laplace mechanism, together with the safe aggregation mannequin and the shuffle model. This doesn’t apply to the extra stringent local DP model, and it stays an attention-grabbing open query to plan sensible native DP heatmap/EMD aggregation algorithms for “average” variety of customers and privateness parameters.
Acknowledgments
This work was performed collectively with Junfeng He, Kai Kohlhoff, Ravi Kumar, Pasin Manurangsi, and Vidhya Navalpakkam.








