A Python Engineer’s Introduction to 3D Gaussian Splatting (Half 3) | by Derek Austin | Jul, 2024
Lastly, we attain essentially the most intriguing part of the Gaussian splatting course of: rendering! This step is arguably essentially the most essential, because it determines the realism of our mannequin. But, it may additionally be the only. In part 1 and part 2 of our sequence we demonstrated methods to remodel uncooked splats right into a format prepared for rendering, however now we truly should do the work and render onto a hard and fast set of pixels. The authors have developed a quick rendering engine utilizing CUDA, which could be considerably difficult to observe. Due to this fact, I imagine it’s helpful to first stroll by means of the code in Python, utilizing simple for loops for readability. For these wanting to dive deeper, all the required code is offered on our GitHub.
Let’s talk about methods to render every particular person pixel. From our earlier article, we’ve got all the required elements: 2D factors, related colours, covariance, sorted depth order, inverse covariance in 2D, minimal and most x and y values for every splat, and related opacity. With these elements, we will render any pixel. Given particular pixel coordinates, we iterate by means of all splats till we attain a saturation threshold, following the splat depth order relative to the digital camera airplane (projected to the digital camera airplane after which sorted by depth). For every splat, we first examine if the pixel coordinate is inside the bounds outlined by the minimal and most x and y values. This examine determines if we must always proceed rendering or ignore the splat for these coordinates. Subsequent, we compute the Gaussian splat power on the pixel coordinate utilizing the splat imply, splat covariance, and pixel coordinates.
def compute_gaussian_weight(
pixel_coord: torch.Tensor, # (1, 2) tensor
point_mean: torch.Tensor,
inverse_covariance: torch.Tensor,
) -> torch.Tensor:distinction = point_mean - pixel_coord
energy = -0.5 * distinction @ inverse_covariance @ distinction.T
return torch.exp(energy).merchandise()
We multiply this weight by the splat’s opacity to acquire a parameter known as alpha. Earlier than including this new worth to the pixel, we have to examine if we’ve got exceeded our saturation threshold. We don’t want a splat behind different splats to have an effect on the pixel coloring and use computing sources if the pixel is already saturated. Thus, we use a threshold that enables us to cease rendering as soon as it’s exceeded. In apply, we begin our saturation threshold at 1 after which multiply it by min(0.99, (1 — alpha)) to get a brand new worth. If this worth is lower than our threshold (0.0001), we cease rendering that pixel and contemplate it full. If not, we add the colours weighted by the saturation * (1 — alpha) worth and replace the saturation as new_saturation = old_saturation * (1 — alpha). Lastly, we loop over each pixel (or each 16×16 tile in apply) and render. The whole code is proven beneath.
def render_pixel(
self,
pixel_coords: torch.Tensor,
points_in_tile_mean: torch.Tensor,
colours: torch.Tensor,
opacities: torch.Tensor,
inverse_covariance: torch.Tensor,
min_weight: float = 0.000001,
) -> torch.Tensor:
total_weight = torch.ones(1).to(points_in_tile_mean.system)
pixel_color = torch.zeros((1, 1, 3)).to(points_in_tile_mean.system)
for point_idx in vary(points_in_tile_mean.form[0]):
level = points_in_tile_mean[point_idx, :].view(1, 2)
weight = compute_gaussian_weight(
pixel_coord=pixel_coords,
point_mean=level,
inverse_covariance=inverse_covariance[point_idx],
)
alpha = weight * torch.sigmoid(opacities[point_idx])
test_weight = total_weight * (1 - alpha)
if test_weight < min_weight:
return pixel_color
pixel_color += total_weight * alpha * colours[point_idx]
total_weight = test_weight
# in case we by no means attain saturation
return pixel_color
Now that we will render a pixel we will render a patch of a picture, or what the authors discuss with as a tile!
def render_tile(
self,
x_min: int,
y_min: int,
points_in_tile_mean: torch.Tensor,
colours: torch.Tensor,
opacities: torch.Tensor,
inverse_covariance: torch.Tensor,
tile_size: int = 16,
) -> torch.Tensor:
"""Factors in tile must be organized so as of depth"""tile = torch.zeros((tile_size, tile_size, 3))
# iterate by tiles for extra environment friendly processing
for pixel_x in vary(x_min, x_min + tile_size):
for pixel_y in vary(y_min, y_min + tile_size):
tile[pixel_x % tile_size, pixel_y % tile_size] = self.render_pixel(
pixel_coords=torch.Tensor([pixel_x, pixel_y])
.view(1, 2)
.to(points_in_tile_mean.system),
points_in_tile_mean=points_in_tile_mean,
colours=colours,
opacities=opacities,
inverse_covariance=inverse_covariance,
)
return tile
And eventually we will use all of these tiles to render a complete picture. Word how we examine to ensure the splat will truly have an effect on the present tile (x_in_tile and y_in_tile code).
def render_image(self, image_idx: int, tile_size: int = 16) -> torch.Tensor:
"""For every tile should examine if the purpose is within the tile"""
preprocessed_scene = self.preprocess(image_idx)
peak = self.pictures[image_idx].peak
width = self.pictures[image_idx].widthpicture = torch.zeros((width, peak, 3))
for x_min in tqdm(vary(0, width, tile_size)):
x_in_tile = (x_min >= preprocessed_scene.min_x) & (
x_min + tile_size <= preprocessed_scene.max_x
)
if x_in_tile.sum() == 0:
proceed
for y_min in vary(0, peak, tile_size):
y_in_tile = (y_min >= preprocessed_scene.min_y) & (
y_min + tile_size <= preprocessed_scene.max_y
)
points_in_tile = x_in_tile & y_in_tile
if points_in_tile.sum() == 0:
proceed
points_in_tile_mean = preprocessed_scene.factors[points_in_tile]
colors_in_tile = preprocessed_scene.colours[points_in_tile]
opacities_in_tile = preprocessed_scene.sigmoid_opacity[points_in_tile]
inverse_covariance_in_tile = preprocessed_scene.inverse_covariance_2d[
points_in_tile
]
picture[x_min : x_min + tile_size, y_min : y_min + tile_size] = (
self.render_tile(
x_min=x_min,
y_min=y_min,
points_in_tile_mean=points_in_tile_mean,
colours=colors_in_tile,
opacities=opacities_in_tile,
inverse_covariance=inverse_covariance_in_tile,
tile_size=tile_size,
)
)
return picture
In the end now that we’ve got all the required elements we will render a picture. We take all of the 3D factors from the treehill dataset and initialize them as gaussian splats. With the intention to keep away from a expensive nearest neighbor search we initialize all scale variables as .01 (Word that with such a small variance we are going to want a powerful focus of splats in a single spot to be seen. Bigger variance makes the method fairly sluggish.). Then all we’ve got to do is name render_image with the picture quantity we are attempting to emulate and as you an see we get a sparse set of level clouds that resemble our picture! (Take a look at our bonus part on the backside for an equal CUDA kernel utilizing pyTorch’s nifty device that compiles CUDA code!)
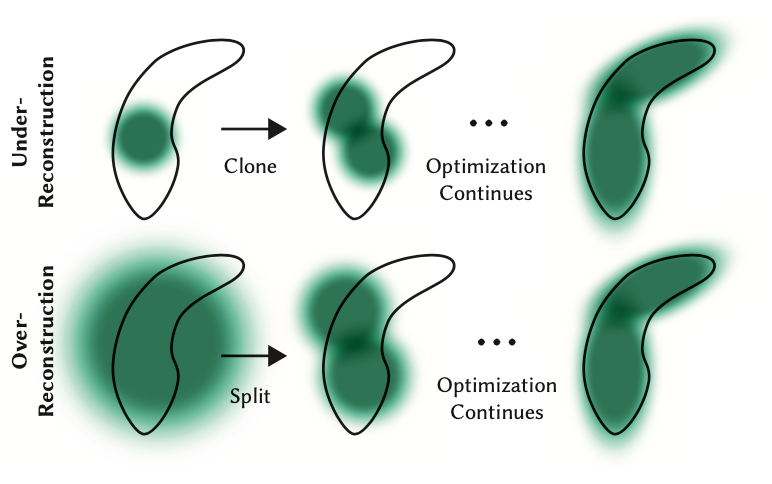
Whereas the backwards cross is just not a part of this tutorial, one notice must be made that whereas we begin with solely these few factors, we quickly have tons of of hundreds of splats for many scenes. That is attributable to the breaking apart of enormous splats (as outlined by bigger variance on axes) into smaller splats and eradicating splats which have extraordinarily low opacity. As an illustration, if we really initialized the dimensions to the imply of the three closest nearest neighbors we might have a majority of the area lined. With the intention to get nice element we would want to interrupt these down into a lot smaller splats which can be in a position to seize nice element. In addition they have to populate areas with only a few gaussians. They refer to those two situations as over reconstruction and underneath reconstruction and outline each situations by massive gradient values for varied splats. They then cut up or clone the splats relying on measurement (see picture beneath) and proceed the optimization course of.
Though the backward cross is just not lined on this tutorial, it’s vital to notice that we begin with just a few factors however quickly have tons of of hundreds of splats in most scenes. This improve is because of the splitting of enormous splats (with bigger variances on axes) into smaller ones and the elimination of splats with very low opacity. As an illustration, if we initially set the dimensions to the imply of the three nearest neighbors, many of the area can be lined. To attain nice element, we have to break these massive splats into a lot smaller ones. Moreover, areas with only a few Gaussians must be populated. These situations are known as over-reconstruction and under-reconstruction, characterised by massive gradient values for varied splats. Relying on their measurement, splats are cut up or cloned (see picture beneath), and the optimization course of continues.
And that’s a straightforward introduction to Gaussian Splatting! You need to now have a great instinct on what precisely is occurring within the ahead cross of a gaussian scene render. Whereas a bit daunting and never precisely neural networks, all it takes is a little bit of linear algebra and we will render 3D geometry in 2D!
Be at liberty to depart feedback about complicated matters or if I bought one thing flawed and you may all the time join with me on LinkedIn or twitter!





