Optimizing LLM Take a look at-Time Compute Entails Fixing a Meta-RL Drawback – Machine Studying Weblog | ML@CMU
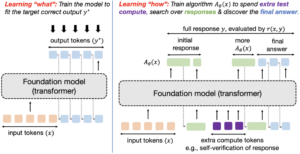
TL;DR: Coaching fashions to optimize test-time compute and study “the way to uncover” appropriate responses, versus the normal studying paradigm of studying “what reply” to output can fashions to raised use knowledge.
The key technique to enhance giant language fashions (LLMs) to this point has been to make use of increasingly more high-quality knowledge for supervised fine-tuning (SFT) or reinforcement studying (RL). Sadly, it appears this type of scaling will quickly hit a wall, with the scaling legal guidelines for pre-training plateauing, and with studies that high-quality textual content knowledge for coaching perhaps exhausted by 2028, significantly for tougher duties, like fixing reasoning issues which appears to require scaling current data by about 100x to see any important enchancment. The present efficiency of LLMs on issues from these laborious duties stays underwhelming (see example). There’s thus a urgent want for data-efficient strategies for coaching LLMs that stretch past knowledge scaling and may tackle extra advanced challenges. On this publish, we are going to talk about one such strategy: by altering the LLM coaching goal, we are able to reuse current knowledge together with extra test-time compute to coach fashions to do higher.
Present LLMs are Skilled on “What” to Reply
The predominant precept for coaching fashions as we speak is to oversee them into producing a sure output for an enter. As an illustration, supervised fine-tuning makes an attempt to match direct output tokens given an enter akin to imitation studying and RL fine-tuning trains the response to optimize a reward perform that’s sometimes purported to take the very best worth on an oracle response. In both case, we’re coaching the mannequin to supply the very best approximation to (y^star) it might characterize. Abstractly, this paradigm trains fashions to supply a single input-output mapping, which works properly when the purpose is to instantly resolve a set of comparable queries from a given distribution, however fails to find options to out-of-distribution queries. A hard and fast, one-size-fits-all strategy can not adapt to the duty heterogeneity successfully. We’d as a substitute need a strong mannequin that is ready to generalize to new, unseen issues by attempting a number of approaches and in search of info to completely different extents, or expressing uncertainty when it’s absolutely unable to totally resolve an issue. How can we practice fashions to fulfill these desiderata?
Studying “Easy methods to Reply” Can Generalize Past
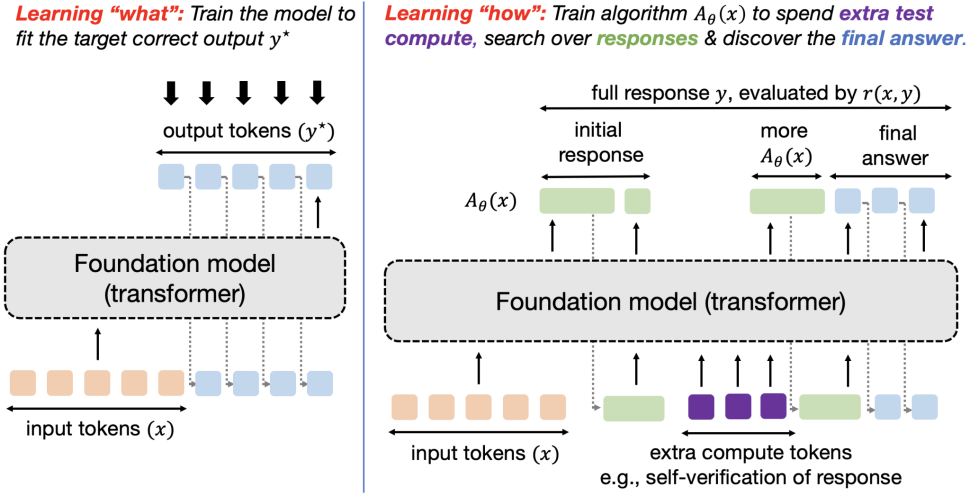
To handle the above concern, one rising concept is to permit fashions to make use of test-time compute to search out “meta” methods or algorithms that may assist them perceive “how” to reach at an excellent response. In case you are new to test-time compute take a look at these papers, this glorious overview talk by Sasha Rush, and the NeurIPS tutorial by Sean Welleck et al. Implementing meta strategies that imbue a mannequin with the potential of working a scientific process to reach at a solution ought to allow extrapolation and generalization to enter queries of various complexities at check time. As an illustration, if a mannequin is taught what it means to make use of the Cauchy-Schwarz inequality, it ought to be capable to invoke it on the proper time on each straightforward and laborious proof issues (doubtlessly by guessing its utilization, adopted by a trial-and-error try and see if it may be utilized in a given downside). In different phrases, given a check question, we wish fashions to be able to executing methods that contain a number of atomic items of reasoning (e.g., a number of era and verification makes an attempt; a number of partially-completed options akin to look; and so on) which seemingly come at the price of spending extra tokens. See Determine 2 for an instance of two completely different methods to assault a given downside. How can we practice fashions to take action? We are going to formalize this purpose right into a studying downside and resolve it by way of concepts from meta RL.

Determine 2: Examples of two algorithms and the corresponding stream of tokens generated by every algorithm. This contains tokens which might be used to fetch related info from the mannequin weights, plan the proof define, confirm intermediate outcomes, and revise if wanted. The primary algorithm (left) generates an preliminary resolution, verifies its correctness and revises if wanted. The second algorithm (proper) generates a number of resolution methods directly, and runs by means of every of them in a linear style earlier than selecting essentially the most promising technique.
Formulating Studying “How” as an Goal
For each downside (x in mathcal{X}), say we’ve a reward perform (r(x, cdot): mathcal{Y} mapsto {0,1}) that we are able to question on any output stream of tokens (y). For e.g., on a math reasoning downside (x), with token output stream (y), reward (r(x, y)) will be one which checks if some subsequence of tokens accommodates the proper reply. We’re solely given the dataset of coaching issues (mathcal{D}_mathrm{practice}), and consequently the set of reward features ({r(x, cdot) : x in mathcal{D}_mathrm{practice}}). Our purpose is to attain excessive rewards on the distribution of check issues (mathcal{P}_text{check}), that are unknown apriori. The check issues will be of various issue in comparison with practice issues.
For an unknown distribution of check issues (mathcal{P}_mathrm{check}), and a finite test-time compute funds (C), we are able to study an algorithm (A in mathcal{A}_C (mathcal{D}_mathrm{practice})) within the inference compute-constrained class of test-time algorithms (mathcal{A}_C) realized from the dataset of coaching issues (mathcal{D}_mathrm{practice}). Every algorithm on this class takes as enter the issue (x sim mathcal{P}_mathrm{check}), and outputs a stream of tokens. In Determine 2, we give some examples to construct instinct for what this stream of tokens will be. As an illustration, (A_theta(x)) may include tokens that first correspond to some try at downside (x), then some verification tokens which predict the correctness of the try, adopted by some refinement of the preliminary try (if verified to be incorrect), all stitched collectively in a “linear” style. One other algorithm (A_theta(x)) may very well be one which simulates some type of heuristic-guided search in a linear style. The category of algorithms (mathcal{A}_C(mathcal{D}_mathrm{practice})) would then include subsequent token distributions induced by all attainable (A_theta(x)) above. Notice that in every of those examples, we hope to make use of extra tokens to study a generic however generalizing process versus guessing the answer to the issue (x).
Our studying purpose is to study (A_theta(x)) , parameterized by an autoregressive LLM (A_theta(x)) (see Determine 1 for an illustration of tokens from (A_theta)). We confer with this whole stream (together with the ultimate reply) as a response (y sim A_theta(x)). The utility of algorithm (A_theta(x)) is given by its common correctness as measured by reward (r(x, y)). Therefore, we are able to pose studying an algorithm as fixing the next optimization downside:
$$max_{A_theta in mathcal{A}_C (mathcal{D}_text{practice})} ; mathbb{E}_{x sim mathcal{P}_mathrm{check}} [ mathbb{E}_{y sim A_theta(x)} r(x, y) ; | ; mathcal{D}_text{train}] ~~~~~~~~~~ textual content{(Optimize “How” or Op-How)}.$$
Deciphering (Op-How) as a Meta RL Drawback
The subsequent query is: how can we resolve the optimization downside (Op-How) over the category of compute-constrained algorithms (mathcal{A_c}), parameterized by a language mannequin? Clearly, we have no idea the outcomes for nor have any supervision for check issues. So, computing the outer expectation is futile. A customary LLM coverage that guesses the very best response for downside (x) additionally appears suboptimal as a result of it may do higher if it made full use of compute funds (C.) The principle concept is that algorithms (A_theta(x) in mathcal{A}_c) that optimize (Op-How) resemble an adaptive policy in RL that makes use of the extra token funds to implement some type of an algorithmic technique to unravel the enter downside (x) (type of like “in-context search” or “in-context exploration”). With this connection, we are able to take inspiration from how comparable issues have been solved sometimes: by viewing (Op-How) by means of the lens of meta studying, particularly, meta RL: “meta” as we want to study algorithms and never direct solutions to given issues & “RL” since (Op-How) is a reward maximization downside.
A really, very brief primer on meta RL. Sometimes, RL trains a coverage to maximise a given reward perform in a Markov choice course of (MDP). In distinction, the meta RL downside setting assumes entry to a distribution of duties (that every admit completely different reward features and dynamics). The purpose on this setting is to coach the coverage on duties from this coaching distribution, such that it might do properly on the check job drawn from the identical or a unique check distribution. Moreover, this setting doesn’t consider this coverage when it comes to its zero-shot efficiency on the check job, however lets it adapt to the check job by executing a number of “coaching” episodes at test-time, after executing which the coverage is evaluated. Most meta RL strategies differ within the design of the variation process (e.g., (text{RL}^2) parameterizes this adaptation process by way of in-context RL; MAML runs specific gradient updates at check time; PEARL adapts a latent variable figuring out the duty). We refer readers to this survey for extra particulars.
Coming again to our setting, you may be questioning the place the Markov choice course of (MDP) and a number of duties (for meta RL) are available in. Each downside (x in mathcal{X}) induces a brand new RL job formalized as a Markov Choice Course of (MDP) (M_x) with the set of tokens in the issue (x) because the preliminary state, each token produced by our LLM denoted by (A_theta(x)) as an motion, and trivial deterministic dynamics outlined by concatenating new tokens (in mathcal{T}) with the sequence of tokens to this point. Notice, that every one MDPs share the set of actions and in addition the set of states (mathcal{S} = mathcal{X} instances cup_{h=1}^{H} mathcal{T}^h), which correspond to variable-length token sequences attainable within the vocabulary. Nevertheless, every MDP (M_x) admits a unique unknown reward perform given by the comparator (r(x, cdot)).
Then fixing (Op-How) corresponds to discovering a coverage that may rapidly adapt to the distribution of check issues (or check states) inside the compute funds (C). One other technique to view this notion of test-time generalization is thru the lens of prior work known as the epistemic POMDP, a assemble that views studying a coverage over household of (M_x) as a partially-observed RL downside. This angle supplies one other technique to encourage the necessity for adaptive insurance policies and meta RL: for individuals who come from an RL background, it shouldn’t be shocking that solving a POMDP is equivalent to running meta RL. Therefore, by fixing a meta RL goal, we’re in search of the optimum coverage for this epistemic POMDP and allow generalization.
Earlier than we go into specifics, a pure query to ask is why this meta RL perspective is fascinating or helpful, since meta RL is known to be hard. We consider that whereas studying insurance policies from scratch fully by way of meta RL is difficult, when utilized to fine-tuning fashions that come outfitted with wealthy priors out of pre-training, meta RL impressed concepts will be useful. As well as, the meta RL downside posed above displays particular construction (recognized and deterministic dynamics, completely different preliminary states), enabling us to develop non-general however helpful meta RL algorithms.
How can the adaptive coverage (LLM (A_theta)) adapt to a check downside (MDP (M_x))?
In meta RL, for every check MDP (M_x), the coverage (A_theta) is allowed to realize info by spending test-time compute, earlier than being evaluated on the ultimate response generated by (A_theta). Within the meta RL terminology, the data gained in regards to the check MDP (M_x) will be considered amassing rewards on coaching episodes of the MDP induced by the check downside (x), earlier than being evaluated on the check episode (see (text{RL}^2) paper; Part 2.2). Notice that every one of those episodes are carried out as soon as the mannequin is deployed. Due to this fact, with a view to resolve (Op-How), we are able to view your entire stream of tokens from (A_theta(x)) as a stream cut up into a number of coaching episodes. For the test-time compute to be optimized, we have to be sure that every episode supplies some information gain to do higher within the subsequent episode of the check MDP (M_x). If there is no such thing as a info acquire, then studying (A_theta(x)) drops right down to an ordinary RL downside — with a better compute funds — and it turns into unclear if studying how is helpful in any respect.
What sort of info will be gained? In fact, if exterior interfaces are concerned inside the stream of tokens we may get extra info. Nevertheless, are we exploiting free lunch if no exterior instruments are concerned? We comment that this isn’t the case and no exterior instruments should be concerned with a view to acquire info because the stream of tokens progresses. Every episode in a stream may meaningfully add extra info (for e.g., with separately-trained verifiers, or self-verification, performed by (A_theta) itself) by sharpening the mannequin’s posterior perception over the true reward perform (r(x, cdot)) and therefore the optimum response (y^star). That’s, we are able to view spending extra test-time compute as a method of sampling from the mannequin’s approximation of the posterior over the optimum resolution (P(cdot mid x, theta)), the place every episode (or token within the output stream) refines this approximation. Thus, explicitly conditioning on previously-generated tokens can present a computationally possible method of representing this posterior with a hard and fast measurement LLM. This additionally implies that even within the absence of exterior inputs, we anticipate the mutual info (I(r(x, cdot); textual content{tokens to date}|x)) or (I(y^star; textual content{tokens to date}|x)) to extend because the extra tokens are produced by (A_theta(x)).
For instance, let’s contemplate the response (A_theta(x)) that features natural language verification tokens (see generative RMs) that assess intermediate generations. On this case, since all supervision comes from (A_theta) itself, we want an asymmetry between era and verification for verification to induce info acquire. One other concept is that when a mannequin underfits on its coaching knowledge, merely an extended size may additionally be capable to present important info acquire on account of a rise in capability (see Part 2 here). Whereas actually extra work is required to formalize these arguments, there are already some works on self-improvement that implicitly or explicitly exploit this asymmetry.
Placing it collectively, when considered as a meta RL downside (A(cdot|cdot)) turns into a history-conditioned (“adaptive”) coverage that optimizes reward (r) by spending computation of as much as (C) on a given check downside. Studying an adaptive coverage conditioned on previous episodes is exactly the purpose of black-box meta-reinforcement studying strategies. Meta RL can also be carefully tied to the query of studying the way to discover, and one can certainly view these further tokens as offering strategic exploration for a given downside.

Determine 3: Agent-environment interplay protocol from the (textual content{RL}^2) paper. Every check downside (x) casts a brand new MDP (M_x). On this MDP, the agent interacts with the surroundings over a number of episodes. In our setting, which means that the stream of tokens in (A_theta(x)) includes of a number of episodes, the place (A_theta(x) ) makes use of the compute funds in every episode to realize details about the underlying MDP (M_x). All of the gained info goes into the historical past (h_i), which evolves throughout the span of all of the episodes. The algorithm (A_theta(x)) is skilled to gather significant historical past in a hard and fast compute funds to have the ability to output a remaining reply that achieves excessive rewards in MDP (M_x).
Studying Adaptive Insurance policies by way of Meta RL: Challenges & Algorithms

Determine 4: The response from this specific (A_theta(x)) features a stream of tokens, the place the data acquire (I(r(x, cdot); textual content{tokens to date})) will increase as we pattern extra tokens.
How can we resolve such a meta RL downside? Maybe the obvious strategy to unravel meta RL issues is to make use of black-box meta RL strategies similar to (textual content{RL}^2). This might contain maximizing the sum of rewards over the imagined “episodes” within the output hint (A_theta(x)). As an illustration, if (A_theta(x)) corresponds to utilizing a self-correction technique, the reward for every episode would grade particular person responses showing within the hint as proven on this prior work. If (A_theta(x)) as a substitute prescribes a method that alternates between era and generative verification, then rewards would correspond to success of era and verification. We are able to then optimize:
$$max_theta ~mathbb{E}_{x sim mathcal{D}_text{practice}, y sim A_theta(cdot|x)} left[ sum_{i=1}^{k} underbrace{tilde{r}_i(x, y_{j_{i-1}:j_{i}})}_{text{intermediate process reward}} + alpha cdot underbrace{r(x, y)}_{text{final correctness}} right]~~~~~~~ textual content{(Obj-1)},$$
the place ({ j_i }_{i=1}^{ok}) correspond to indices of the response that truncate the episodes marked and reward (tilde{r}_i) corresponds to a scalar reward sign for that episode (e.g., verification correctness for a verification section, era correctness for a era section, and so on.) and as well as, we optimize the ultimate correctness reward of the answer weighted by (alpha). Notice that this formulation prescribes a dense, process-based reward for studying (observe that this isn’t equal to utilizing a step-level course of reward mannequin (PRM), however a dense reward bonus as a substitute; connection between such dense reward bonuses and exploration will be present in this prior paper). As well as, we are able to select to constrain the utilization of compute by (A_theta(x)) to an higher certain (C) both explicitly by way of a loss time period or implicitly (e.g., by chopping off the mannequin’s generations that violate this funds).
The above paragraph is particular to era and verification, and normally, the stream of output tokens will not be cleanly separable into era and verification segments. In such settings, one may contemplate the extra summary type of the meta RL downside, which makes use of some estimate of knowledge acquire instantly because the reward. One such estimate may very well be the metric used within the QuietSTaR paper, though it’s not clear what the appropriate technique to outline this metric is.
$$max_theta ~mathbb{E}_{x sim mathcal{D}_text{practice}, y sim A_theta(cdot|x)} left[ sum_{i=1}^{k} underbrace{(I(r(x, cdot); y_{:j_{i}}) – I(r(x, cdot); y_{:j_{i-1}}))}_{text{information gain for segment }i} + alpha cdot underbrace{r(x, y)}_{text{final correctness}} right]~~~~~~~ textual content{(Obj-2)}.$$
One can resolve (textual content{(Obj-1) and (Obj-2)}) by way of multi-turn RL approaches similar to these based mostly on coverage gradients with intermediate dense rewards or based mostly on actor-critic architectures (e.g., prior work ArCHer), and even perhaps the selection of RL strategy (value-based vs. policy-based) might not matter so long as one can resolve the optimization downside utilizing some RL algorithm that performs periodic on-policy rollouts.
We may additionally contemplate a unique strategy for devising a meta RL coaching goal: one which solely optimizes reward attained by the check episode (e.g., remaining reply correctness for the final try) and never the practice episodes, thereby avoiding the necessity to quantify info acquire. We consider that this is able to run into challenges of optimizing extraordinarily sparse supervision on the finish of an extended trajectory (consisting of a number of reasoning segments or a number of “episodes” in meta RL terminology) with RL; dense rewards should be able to do better.
Challenges and open questions. There are fairly a number of challenges that we have to resolve to instantiate this concept in apply as we listing under.
- The primary problem lies in generalizing this framework to algorithm parameterizations (A_theta(x)) that produce token sequences don’t meaningfully separate into semantic duties (e.g., era, verification, and so on.). On this case, how can we offer dense rewards (tilde{r}_i)? We speculate that in such a setting (r_i) ought to correspond to some approximation of info acquire in the direction of producing the proper resolution given enter tokens, however it stays to be seen what this info acquire or progress ought to imply.
- Finally, we are going to apply the above process to fine-tune a pre-trained or instruction-tuned mannequin. How can we initialize the mannequin (A_theta(cdot|cdot)) to be such that it might meaningfully produce an algorithm hint and never merely try the enter question instantly? Relatedly, how does the initialization from next-token prediction goal in pre-training or instruction-tuning have an effect on optimizability of both (textual content{(Obj)}) goal above? Previous work has noticed extreme memorization when utilizing supervised fine-tuning to imbue (A_theta(cdot|cdot)) with a foundation to study self-correction behavior. It stays an open query as as to if this problem is exacerbated in essentially the most basic setting and what will be performed to alleviate it.
- Lastly, we observe {that a} essential situation to get meta studying to efficiently work is the presence of ambiguity that it’s attainable to make use of expertise collected on the check job to adapt the coverage to it. It’s unclear what a scientific technique to introduce the above ambiguity is. Maybe one strategy is to make use of a considerable amount of coaching prompts such that there’s little scope for memorizing the coaching knowledge. This might additionally induce a bias in the direction of utilizing extra obtainable compute (C) for enhancing efficiency. Nevertheless it stays unclear what the higher certain on this strategy is.
Takeaways, Abstract, and Limitations
We introduced a connection between optimizing test-time compute for LLMs and meta RL. By viewing the optimization of test-time compute as the issue of studying an algorithm that figures how to unravel queries at check time, adopted by drawing the connection between doing so and meta RL supplied us with coaching goals that may effectively use test-time compute. This angle does doubtlessly present helpful insights with respect to: (1) the position of intermediate course of rewards that correspond to info acquire in optimizing for test-time compute, (2) the position of mannequin collapse and pre-trained initializations in studying meta methods; and (3) the position of asymmetry as being the driving force of test-time enchancment n the absence of exterior suggestions.
In fact, efficiently instantiating formulations listed above would seemingly require particular and perhaps even surprising implementation particulars, that we don’t cowl and may be difficult to understand utilizing the conceptual mannequin mentioned on this publish. The challenges outlined might not cowl the listing of all attainable challenges that come up with this strategy. Nonetheless, we hope that this connection is helpful in formally understanding test-time computation in LLMs.
Acknowledgements. We wish to thank Sasha Rush, Sergey Levine, Graham Neubig, Abhishek Gupta, Rishabh Agarwal, Katerina Fragkiadaki, Sean Welleck, Yi Su, Charlie Snell, Seohong Park, Yifei Zhou, Dzmitry Bahdanau, Junhong Shen, Wayne Chi, Naveen Raman, and Christina Baek for his or her insightful suggestions, criticisms, discussions, and feedback on an earlier model of this publish. We wish to particularly thank Rafael Rafailov for insightful discussions and suggestions on the contents of this weblog.
If you happen to suppose this weblog publish is helpful to your work, please contemplate citing it.
@misc{setlur2025opt,
writer={Setlur, Amrith and Qu, Yuxiao and Zhang, Lunjun and Yang, Matthew and Smith, Virginia and Kumar, Aviral},
title={Optimizing LLM Take a look at-Time Compute Entails Fixing a Meta-RL Drawback,
howpublished = {url{https://weblog.ml.cmu.edu/2025/01/08/optimizing-llm-test-time-compute-involves-solving-a-meta-rl-problem/}},
observe = {CMU MLD Weblog} ,
12 months={2025},
}