WTF is Regularization and What’s it For?


“An oz of prevention is value a pound of treatment” goes the outdated saying, reminding us that it is simpler to cease one thing from occurring within the first place than to restore the injury after it has occurred.
Within the period of synthetic intelligence (AI), this proverb underscores the significance of avoiding potential pitfalls, similar to overfitting, via methods like regularization.
On this article, we are going to uncover regularization by beginning with its basic ideas to its utility utilizing Sci-kit Study(Machine Studying) and Tensorflow(Deep Studying) and witness its transformative energy with real-world datasets by evaluating these outcomes. Let’s begin!
Regularization is a vital idea in machine studying and deep studying that goals to forestall fashions from overfitting.
Overfitting occurs when a mannequin learns the coaching knowledge too properly. The state of affairs reveals your mannequin is simply too good to be true.
Let’s see what overfitting seems to be like.
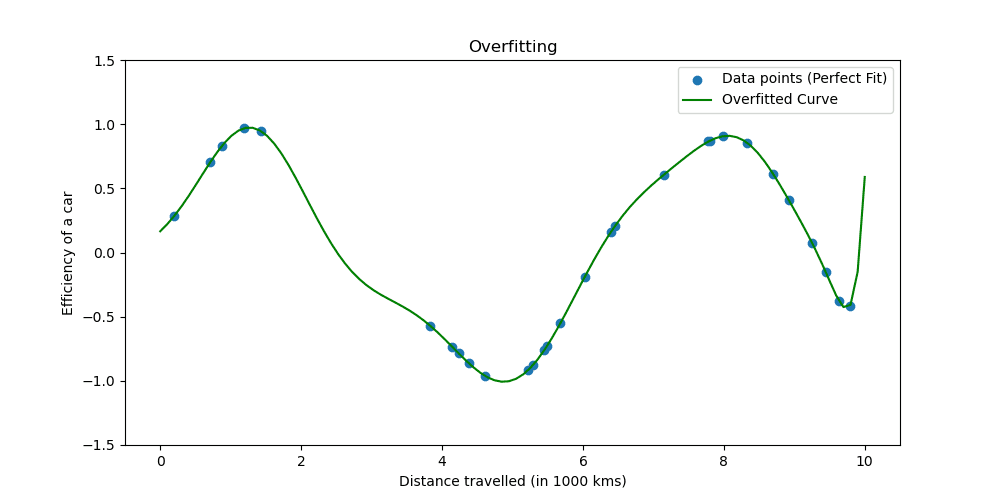
Regularization methods regulate the training course of to simplify the mannequin, making certain it performs properly on coaching knowledge and generalizes properly to new knowledge. We’ll discover two well-known methods of doing this.
In machine studying, regularization is usually utilized to linear fashions, similar to linear and logistic regression. On this context, the commonest types of regularization are:
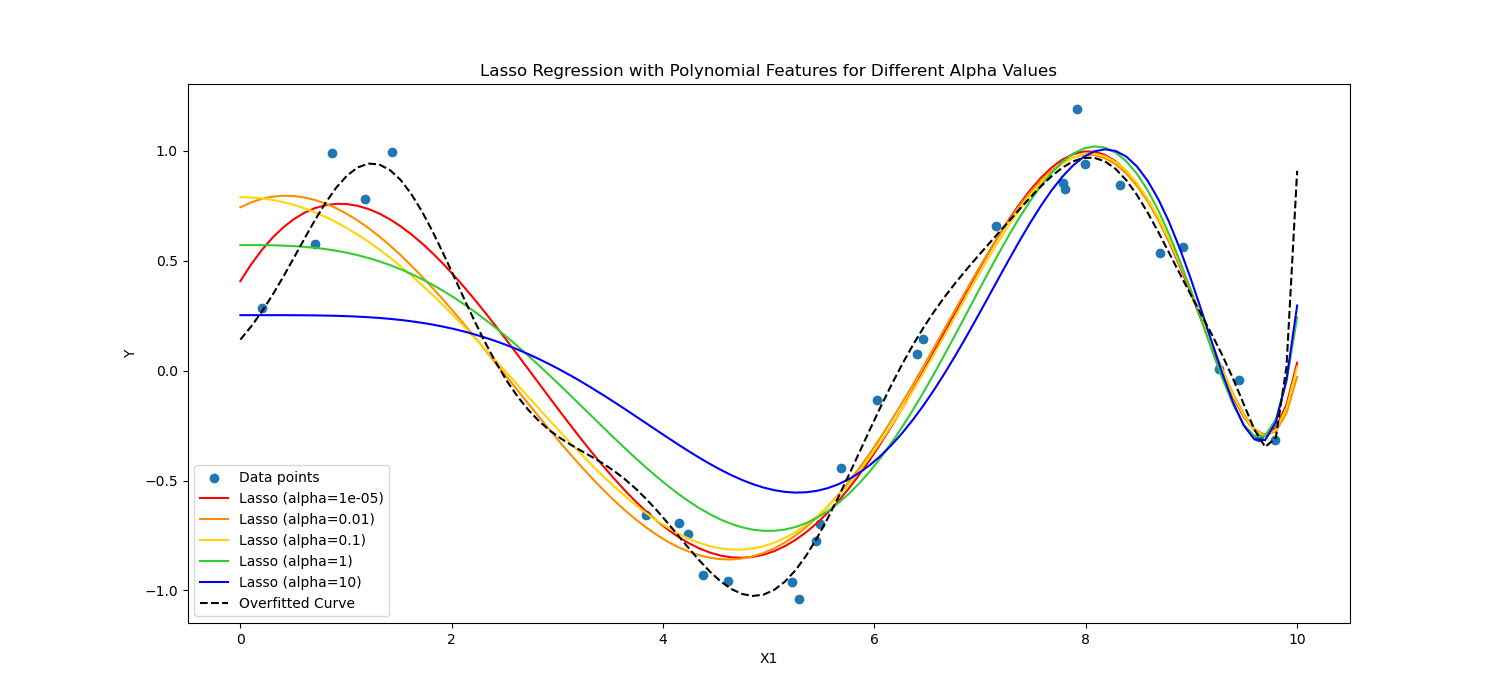
- L1 regularization (Lasso regression)
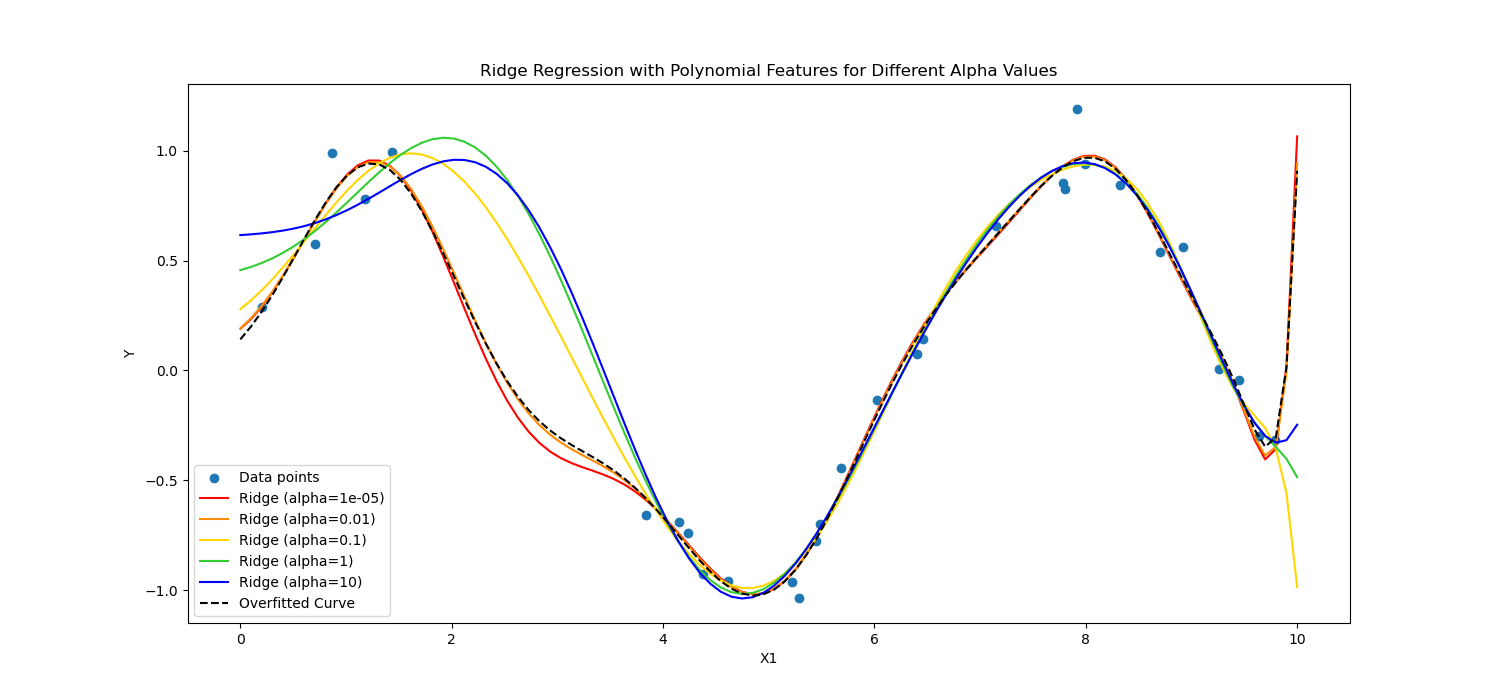
- L2 regularization (Ridge regression)
Lasso Regularization encourages the mannequin to make use of solely essentially the most important options by permitting some coefficient values to be precisely zero, which will be significantly helpful for function choice.
Alternatively, Ridge regularization discourages vital coefficients by penalizing the sq. of their values.
In brief, they calculated in a different way.
Let’s apply these to the cardiac affected person knowledge to see its energy In deep studying and machine studying.
Now, we are going to apply regularization to investigate cardiac affected person knowledge to see the facility of regularization. You possibly can attain the dataset from here.
To use machine studying, we are going to use Scikit-learn; to use deep studying, we are going to use TensorFlow. Let’s begin!
Regularization in Machine Studying
Scikit-learn is among the hottest Python libraries for machine studying that gives easy and environment friendly knowledge evaluation and modeling instruments.
It contains implementations of varied regularization methods, significantly for linear fashions.
Right here, we’ll discover apply L1 (Lasso) and L2 (Ridge) regularization.
Within the following code, we are going to practice logistic regression utilizing Ridge(L2) and Lasso regularization (L1) methods. On the finish, we are going to see the detailed report. Let’s see the code.
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score, classification_report
# Assuming heart_data is already loaded
X = heart_data.drop('goal', axis=1)
y = heart_data['target']
# Cut up the information into coaching and testing units
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# Standardize the options
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_test_scaled = scaler.remodel(X_test)
# Outline regularization values to discover
regularization_values = [0.001, 0.01, 0.1]
# Placeholder for storing efficiency metrics
performance_metrics = []
# Iterate over regularization values for L1 and L2
for C_value in regularization_values:
# Practice and consider L1 mannequin
log_reg_l1 = LogisticRegression(penalty='l1', C=C_value, solver="liblinear")
log_reg_l1.match(X_train_scaled, y_train)
y_pred_l1 = log_reg_l1.predict(X_test_scaled)
accuracy_l1 = accuracy_score(y_test, y_pred_l1)
report_l1 = classification_report(y_test, y_pred_l1)
performance_metrics.append(('L1', C_value, accuracy_l1))
# Practice and consider L2 mannequin
log_reg_l2 = LogisticRegression(penalty='l2', C=C_value, solver="liblinear")
log_reg_l2.match(X_train_scaled, y_train)
y_pred_l2 = log_reg_l2.predict(X_test_scaled)
accuracy_l2 = accuracy_score(y_test, y_pred_l2)
report_l2 = classification_report(y_test, y_pred_l2)
performance_metrics.append(('L2', C_value, accuracy_l2))
# Print the efficiency metrics for all fashions
print("Mannequin Efficiency Analysis:")
print("--------------------------------")
for metric in performance_metrics:
reg_type, C_value, accuracy = metric
print(f"Regularization: {reg_type}, C: {C_value}, Accuracy: {accuracy:.2f}")
Right here is the output.
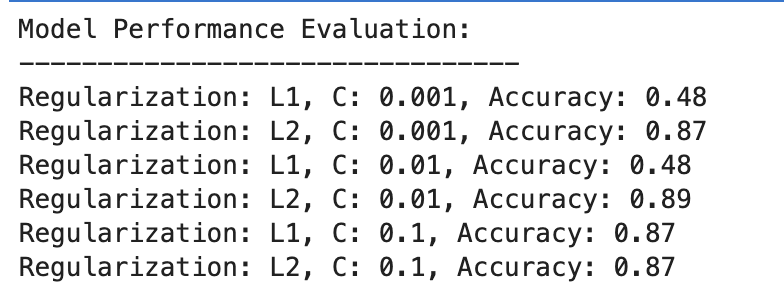
Let’s consider the outcome.
L1 Regularization
- At C=0.001, accuracy is notably low (48%). This reveals that the mannequin is underfitting. It reveals an excessive amount of regularization.
- As C will increase to 0.01, accuracy stays unchanged for L1, suggesting that the mannequin nonetheless suffers from underfitting or the regularization is simply too sturdy.
- At C=0.1, accuracy improves considerably to 87%, displaying that lowering the regularization power permits the mannequin to study higher from the information.
L2 Regularization
Throughout the board, L2 regularization performs constantly properly, with accuracy at 87% for C=0.001 and barely greater at 89% for C=0.01, then stabilizing at 87% for C=0.1.
This implies that L2 regularization is usually extra forgiving and efficient for this dataset in logistic regression fashions, probably resulting from its nature.
Regularization in Deep Studying
A number of regularization methods are utilized in deep studying, together with L1 (Lasso) and L2 (Ridge) regularization, dropout, and early stopping.
On this one, to repeat what we did within the machine studying instance earlier than, we are going to apply L1 and L2 regularization. Let’s outline a listing of L1 and L2 regularization values this time.
Then, for all of those values, we are going to practice and consider our deep studying mannequin, and on the finish, we are going to assess the outcomes.
Let’s see the code.
from tensorflow.keras.regularizers import l1_l2
import numpy as np
# Outline a listing/grid of L1 and L2 regularization values
l1_values = [0.001, 0.01, 0.1]
l2_values = [0.001, 0.01, 0.1]
# Placeholder for storing efficiency metrics
performance_metrics = []
# Iterate over all combos of L1 and L2 values
for l1_val in l1_values:
for l2_val in l2_values:
# Outline mannequin with the present mixture of L1 and L2
mannequin = Sequential([
Dense(128, activation='relu', input_shape=(X_train_scaled.shape[1],), kernel_regularizer=l1_l2(l1=l1_val, l2=l2_val)),
Dropout(0.5),
Dense(64, activation='relu', kernel_regularizer=l1_l2(l1=l1_val, l2=l2_val)),
Dropout(0.5),
Dense(1, activation='sigmoid')
])
mannequin.compile(optimizer="adam", loss="binary_crossentropy", metrics=['accuracy'])
# Practice the mannequin
historical past = mannequin.match(X_train_scaled, y_train, validation_split=0.2, epochs=100, batch_size=10, verbose=0)
# Consider the mannequin
loss, accuracy = mannequin.consider(X_test_scaled, y_test, verbose=0)
# Retailer the efficiency together with the regularization values
performance_metrics.append((l1_val, l2_val, accuracy))
# Discover the most effective performing mannequin
best_performance = max(performance_metrics, key=lambda x: x[2])
best_l1, best_l2, best_accuracy = best_performance
# After the loop, to print all efficiency metrics
print("All Mannequin Performances:")
print("L1 Worth | L2 Worth | Accuracy")
for metrics in performance_metrics:
print(f"{metrics[0]:<8} | {metrics[1]:<8} | {metrics[2]:.3f}")
# After discovering the most effective efficiency, to print the most effective mannequin particulars
print("nBest Mannequin Efficiency:")
print("----------------------------")
print(f"Greatest L1 worth: {best_l1}")
print(f"Greatest L2 worth: {best_l2}")
print(f"Greatest accuracy: {best_accuracy:.3f}")
Right here is the output.
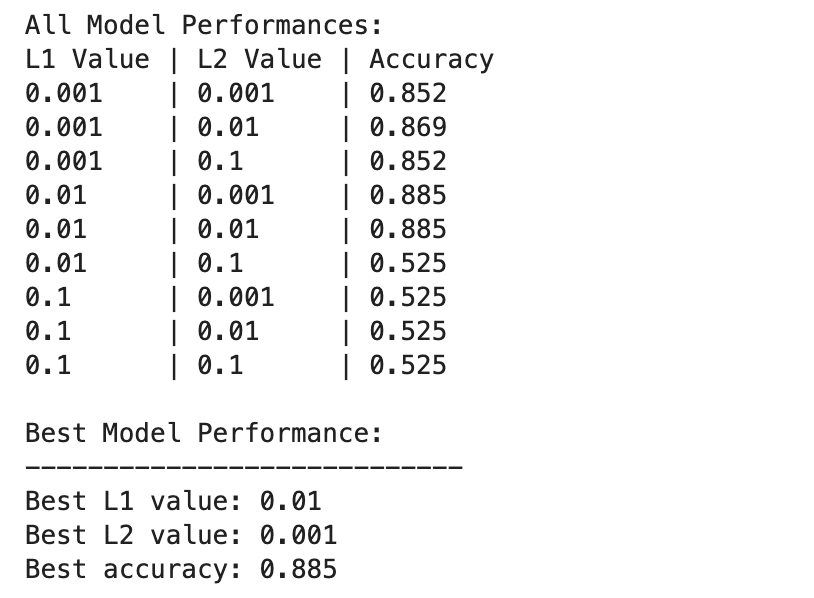
The deep studying mannequin performances range extra broadly throughout totally different combos of L1 and L2 regularization values.
One of the best efficiency is noticed at L1=0.01 and L2=0.001, with an accuracy of 88.5%, which signifies a balanced regularization that forestalls overfitting whereas permitting the mannequin to seize the underlying patterns within the knowledge.
Larger regularization values, particularly at L1=0.1 or L2=0.1, drastically cut back mannequin accuracy to 52.5%, suggesting that an excessive amount of regularization severely limits the mannequin’s studying capability.
Machine Studying & Deep Studying in Regularization
Let’s evaluate the outcomes between Machine Studying and Deep Studying.
Effectiveness of Regularization: Each in machine studying and deep studying contexts, acceptable regularization helps mitigate overfitting, however extreme regularization results in underfitting. The optimum regularization power varies, with deep studying fashions probably requiring a extra nuanced stability resulting from their greater complexity.
Efficiency: One of the best-performing machine studying mannequin (L2 with C=0.01, 89% accuracy) and the best-performing deep studying mannequin (L1=0.01, L2=0.001, 88.5% accuracy) obtain comparable accuracies, demonstrating that each approaches will be successfully regularized to realize excessive efficiency on this dataset.
Regularization Technique: L2 regularization seems to be simpler and fewer delicate to the selection of C in logistic regression fashions, whereas a mix of L1 and L2 regularization gives the most effective end in deep studying, providing a stability between function choice and weight penalization.
The selection and power of regularization must be rigorously tuned to stability studying complexity with the chance of overfitting or underfitting.
All through this exploration, we have demystified regularization, displaying its position in stopping overfitting and making certain our fashions generalize properly to unseen knowledge.
Making use of regularization methods will convey you nearer to proficiency in machine studying and deep studying, solidifying your knowledge scientist toolset.
Go into the information tasks and check out regularizing your knowledge in numerous situations, similar to Delivery Duration Prediction. We used each Machine Studying and Deep Studying fashions on this knowledge challenge. Nonetheless, ultimately, we additionally talked about that there is likely to be room for enchancment. So why don’t you strive regularization over there and see if it helps?
Nate Rosidi is an information scientist and in product technique. He is additionally an adjunct professor instructing analytics, and is the founding father of StrataScratch, a platform serving to knowledge scientists put together for his or her interviews with actual interview questions from prime corporations. Join with him on Twitter: StrataScratch or LinkedIn.