Understanding LoRA — Low Rank Adaptation For Finetuning Massive Fashions | by Bhavin Jawade | Dec, 2023
Effective-tuning massive pre-trained fashions is computationally difficult, typically involving adjustment of hundreds of thousands of parameters. This conventional fine-tuning method, whereas efficient, calls for substantial computational assets and time, posing a bottleneck for adapting these fashions to particular duties. LoRA introduced an efficient resolution to this downside by decomposing the replace matrix throughout finetuing. To check LoRA, allow us to begin by first revisiting conventional finetuing.
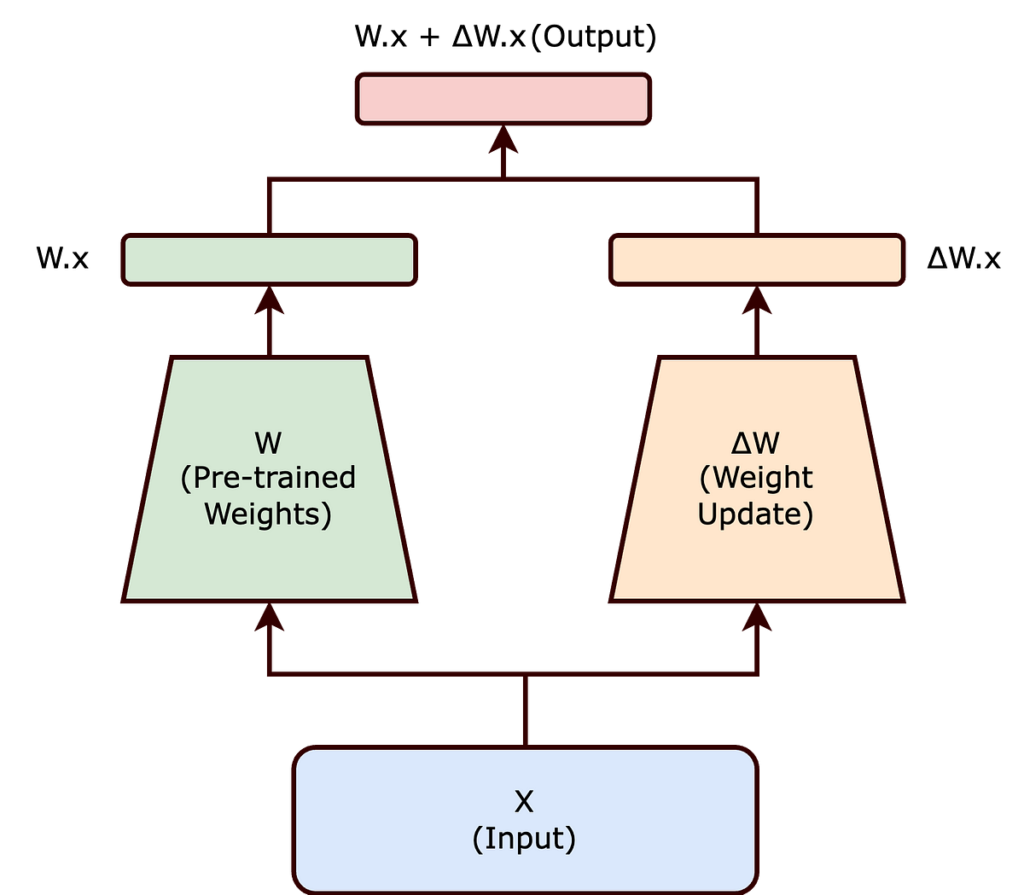
In conventional fine-tuning, we modify a pre-trained neural community’s weights to adapt to a brand new process. This adjustment includes altering the unique weight matrix ( W ) of the community. The adjustments made to ( W ) throughout fine-tuning are collectively represented by ( Δ W ), such that the up to date weights will be expressed as ( W + Δ W ).
Now, relatively than modifying ( W ) immediately, the LoRA method seeks to decompose ( Δ W ). This decomposition is a vital step in lowering the computational overhead related to fine-tuning massive fashions.
The intrinsic rank speculation means that important adjustments to the neural community will be captured utilizing a lower-dimensional illustration. Basically, it posits that not all components of ( Δ W ) are equally necessary; as a substitute, a smaller subset of those adjustments can successfully encapsulate the required changes.
Constructing on this speculation, LoRA proposes representing ( Δ W ) because the product of two smaller matrices, ( A ) and ( B ), with a decrease rank. The up to date weight matrix ( W’ ) thus turns into:
[ W’ = W + BA ]
On this equation, ( W ) stays frozen (i.e., it isn’t up to date throughout coaching). The matrices ( B ) and ( A ) are of decrease dimensionality, with their product ( BA ) representing a low-rank approximation of ( Δ W ).
By selecting matrices ( A ) and ( B ) to have a decrease rank ( r ), the variety of trainable parameters is considerably lowered. For instance, if ( W ) is a ( d x d ) matrix, historically, updating ( W ) would contain ( d² ) parameters. Nonetheless, with ( B ) and ( A ) of sizes ( d x r ) and ( r x d ) respectively, the full variety of parameters reduces to ( 2dr ), which is far smaller when ( r << d ).
The discount within the variety of trainable parameters, as achieved by the Low-Rank Adaptation (LoRA) methodology, provides a number of important advantages, significantly when fine-tuning large-scale neural networks:
- Diminished Reminiscence Footprint: LoRA decreases reminiscence wants by reducing the variety of parameters to replace, aiding within the administration of large-scale fashions.
- Sooner Coaching and Adaptation: By simplifying computational calls for, LoRA accelerates the coaching and fine-tuning of enormous fashions for brand new duties.
- Feasibility for Smaller {Hardware}: LoRA’s decrease parameter depend allows the fine-tuning of considerable fashions on much less highly effective {hardware}, like modest GPUs or CPUs.
- Scaling to Bigger Fashions: LoRA facilitates the enlargement of AI fashions with no corresponding enhance in computational assets, making the administration of rising mannequin sizes extra sensible.
Within the context of LoRA, the idea of rank performs a pivotal position in figuring out the effectivity and effectiveness of the variation course of. Remarkably, the paper highlights that the rank of the matrices A and B will be astonishingly low, generally as little as one.
Though the LoRA paper predominantly showcases experiments inside the realm of Pure Language Processing (NLP), the underlying method of low-rank adaptation holds broad applicability and might be successfully employed in coaching numerous sorts of neural networks throughout totally different domains.
LoRA’s method to decomposing ( Δ W ) right into a product of decrease rank matrices successfully balances the necessity to adapt massive pre-trained fashions to new duties whereas sustaining computational effectivity. The intrinsic rank idea is essential to this steadiness, guaranteeing that the essence of the mannequin’s studying functionality is preserved with considerably fewer parameters.