Instructing language fashions to purpose algorithmically – Google Analysis Weblog

Giant language fashions (LLMs), akin to GPT-3 and PaLM, have proven spectacular progress lately, which have been pushed by scaling up models and training data sizes. Nonetheless, a protracted standing debate has been whether or not LLMs can purpose symbolically (i.e., manipulating symbols based mostly on logical guidelines). For instance, LLMs are in a position to carry out easy arithmetic operations when numbers are small, however battle to carry out with giant numbers. This implies that LLMs haven’t realized the underlying guidelines wanted to carry out these arithmetic operations.

Whereas neural networks have highly effective pattern matching capabilities, they’re susceptible to overfitting to spurious statistical patterns within the information. This doesn’t hinder good efficiency when the coaching information is giant and various and the analysis is in-distribution. Nevertheless, for duties that require rule-based reasoning (akin to addition), LLMs battle with out-of-distribution generalization as spurious correlations within the coaching information are sometimes a lot simpler to take advantage of than the true rule-based answer. In consequence, regardless of vital progress in quite a lot of pure language processing duties, efficiency on easy arithmetic duties like addition has remained a problem. Even with modest enchancment of GPT-4 on the MATH dataset, errors are still largely due to arithmetic and calculation mistakes. Thus, an necessary query is whether or not LLMs are able to algorithmic reasoning, which entails fixing a process by making use of a set of summary guidelines that outline the algorithm.

In “Teaching Algorithmic Reasoning via In-Context Learning”, we describe an method that leverages in-context learning to allow algorithmic reasoning capabilities in LLMs. In-context studying refers to a mannequin’s potential to carry out a process after seeing just a few examples of it throughout the context of the mannequin. The duty is specified to the mannequin utilizing a immediate, with out the necessity for weight updates. We additionally current a novel algorithmic prompting method that permits basic goal language fashions to realize robust generalization on arithmetic issues which can be tougher than these seen within the immediate. Lastly, we reveal {that a} mannequin can reliably execute algorithms on out-of-distribution examples with an applicable alternative of prompting technique.

By offering algorithmic prompts, we will train a mannequin the principles of arithmetic by way of in-context studying. On this instance, the LLM (phrase predictor) outputs the proper reply when prompted with a straightforward addition query (e.g., 267+197), however fails when requested an identical addition query with longer digits. Nevertheless, when the tougher query is appended with an algorithmic immediate for addition (blue field with white + proven beneath the phrase predictor), the mannequin is ready to reply accurately. Furthermore, the mannequin is able to simulating the multiplication algorithm (X) by composing a sequence of addition calculations.

Instructing an algorithm as a talent

As a way to train a mannequin an algorithm as a talent, we develop algorithmic prompting, which builds upon different rationale-augmented approaches (e.g., scratchpad and chain-of-thought). Algorithmic prompting extracts algorithmic reasoning talents from LLMs, and has two notable distinctions in comparison with different prompting approaches: (1) it solves duties by outputting the steps wanted for an algorithmic answer, and (2) it explains every algorithmic step with ample element so there is no such thing as a room for misinterpretation by the LLM.

To achieve instinct for algorithmic prompting, let’s think about the duty of two-number addition. In a scratchpad-style immediate, we course of every digit from proper to left and maintain monitor of the carry worth (i.e., we add a 1 to the subsequent digit if the present digit is bigger than 9) at every step. Nevertheless, the rule of carry is ambiguous after seeing just a few examples of carry values. We discover that together with specific equations to explain the rule of carry helps the mannequin deal with the related particulars and interpret the immediate extra precisely. We use this perception to develop an algorithmic immediate for two-number addition, the place we offer specific equations for every step of computation and describe numerous indexing operations in non-ambiguous codecs.

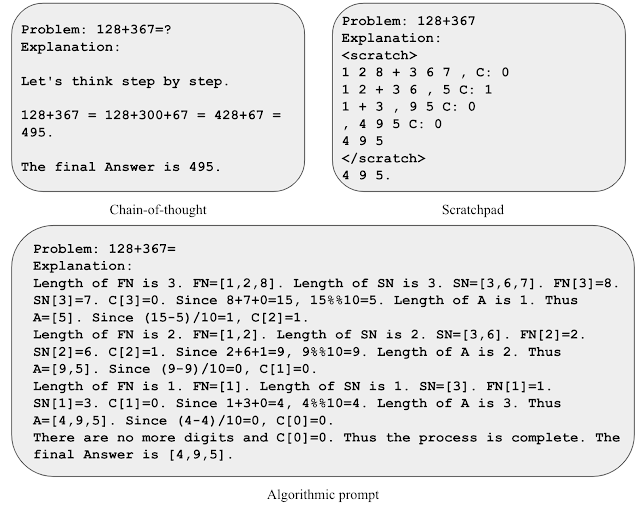Illustration of assorted immediate methods for addition.

Utilizing solely three immediate examples of addition with reply size as much as 5 digits, we consider efficiency on additions of as much as 19 digits. Accuracy is measured over 2,000 whole examples sampled uniformly over the size of the reply. As proven beneath, using algorithmic prompts maintains excessive accuracy for questions considerably longer than what’s seen within the immediate, which demonstrates that the mannequin is certainly fixing the duty by executing an input-agnostic algorithm.

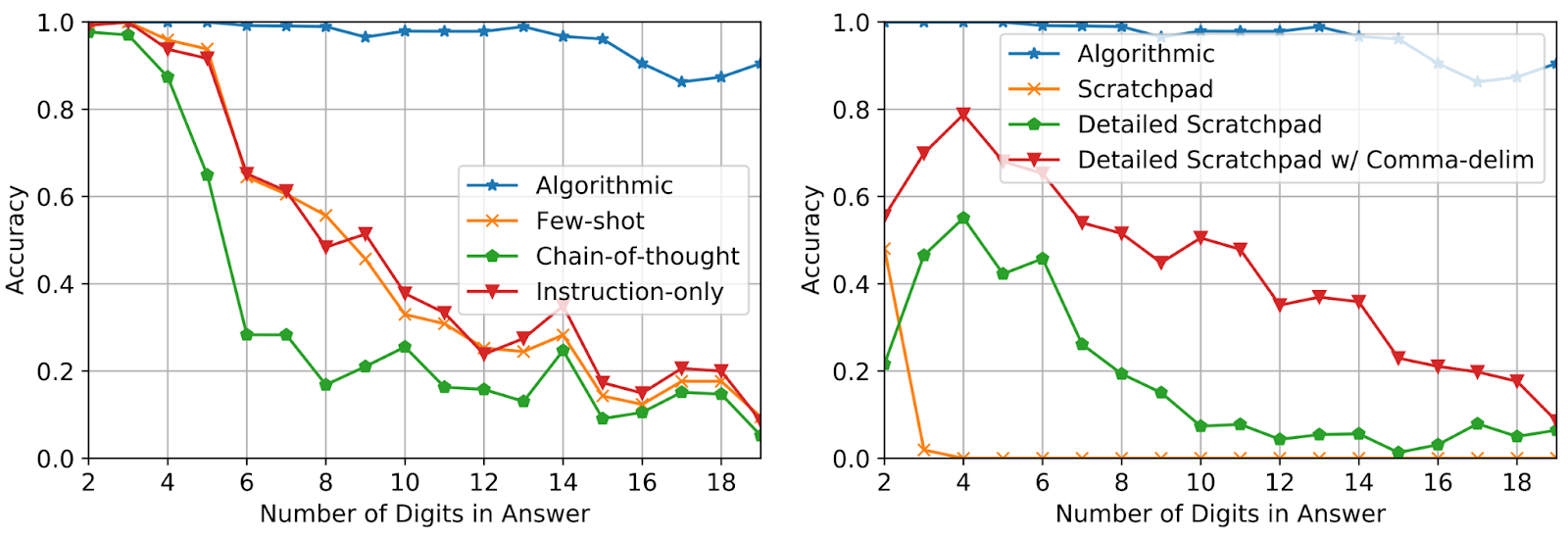Take a look at accuracy on addition questions of accelerating size for various prompting strategies.

Leveraging algorithmic expertise as software use

To judge if the mannequin can leverage algorithmic reasoning in a broader reasoning course of, we consider efficiency utilizing grade faculty math phrase issues (GSM8k). We particularly try to exchange addition calculations from GSM8k with an algorithmic answer.

Motivated by context size limitations and potential interference between totally different algorithms, we discover a technique the place differently-prompted fashions work together with each other to resolve advanced duties. Within the context of GSM8k, we’ve got one mannequin that focuses on casual mathematical reasoning utilizing chain-of-thought prompting, and a second mannequin that focuses on addition utilizing algorithmic prompting. The casual mathematical reasoning mannequin is prompted to output specialised tokens with the intention to name on the addition-prompted mannequin to carry out the arithmetic steps. We extract the queries between tokens, ship them to the addition-model and return the reply to the primary mannequin, after which the primary mannequin continues its output. We consider our method utilizing a troublesome drawback from the GSM8k (GSM8k-Laborious), the place we randomly choose 50 addition-only questions and improve the numerical values within the questions.

An instance from the GSM8k-Laborious dataset. The chain-of-thought immediate is augmented with brackets to point when an algorithmic name must be carried out.

We discover that utilizing separate contexts and fashions with specialised prompts is an efficient method to deal with GSM8k-Laborious. Under, we observe that the efficiency of the mannequin with algorithmic name for addition is 2.3x the chain-of-thought baseline. Lastly, this technique presents an instance of fixing advanced duties by facilitating interactions between LLMs specialised to totally different expertise by way of in-context studying.

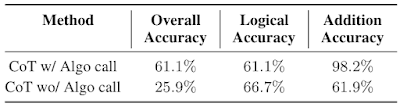Chain-of-thought (CoT) efficiency on GSM8k-Laborious with or with out algorithmic name.

Conclusion

We current an method that leverages in-context learning and a novel algorithmic prompting method to unlock algorithmic reasoning talents in LLMs. Our outcomes counsel that it might be potential to remodel longer context into higher reasoning efficiency by offering extra detailed explanations. Thus, these findings level to the flexibility of utilizing or in any other case simulating lengthy contexts and producing extra informative rationales as promising analysis instructions.

Acknowledgements

We thank our co-authors Behnam Neyshabur, Azade Nova, Hugo Larochelle and Aaron Courville for his or her beneficial contributions to the paper and nice suggestions on the weblog. We thank Tom Small for creating the animations on this publish. This work was completed throughout Hattie Zhou’s internship at Google Analysis.