Vector and Matrix Norms with NumPy Linalg Norm

Picture by Writer
Numerical Python or NumPy is a well-liked library for scientific computing in Python. The NumPy library has an enormous assortment of built-in performance to create n-dimensional arrays and carry out computations on them.
Should you’re serious about information science, computational linear algebra and associated fields, studying methods to compute vector and matrix norms could be useful. And this tutorial will educate you the way to do this utilizing capabilities from NumPy’s linalg module.
To code alongside, you must have Python and NumPy put in in your growth setting. For the f-strings within the print() statements to work with out errors, you want to have Python 3.8 or a later model put in.
Let’s start!
On this dialogue, we’ll first have a look at vector norms. We’ll get to matrix norms later. Mathematically, a norm is a operate (or a mapping) from an n-dimensional vector area to the set of actual numbers:
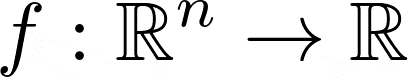
Be aware: Norms are additionally outlined on advanced vector areas C^n → R is a sound definition of norm, too. However we’ll limit ourselves to the vector area of actual numbers on this dialogue.
Properties of Norms
For an n-dimensional vector x = (x1,x2,x3,…,xn), the norm of x, generally denoted by ||x||, ought to fulfill the next properties:
- ||x|| is a non-negative amount. For a vector x, the norm ||x|| is at all times higher than or equal to zero. And ||x|| is the same as zero if and provided that the vector x is the vector of all zeros.
- For 2 vectors x = (x1,x2,x3,…,xn) and y = (y1,y2,y3,…,yn), their norms ||x|| and ||y|| ought to fulfill the triangle inequality: ||x + y|| <= ||x|| + ||y||.
- As well as, all norms fulfill ||αx|| = |α| ||x|| for a scalar α.
Normally, the Lp norm (or p-norm) of an n-dimensional vector x = (x1,x2,x3,…,xn) for p >= 0 is given by:

Let’s check out the frequent vector norms, specifically, the L1, L2 and L∞ norms.
L1 Norm
The L1 norm is the same as the sum of absolutely the values of components within the vector:

L2 Norm
Substituting p =2 within the common Lp norm equation, we get the next expression for the L2 norm of a vector:

L∞ norm
For a given vector x, the L∞ norm is the most of the absolute values of the weather of x:
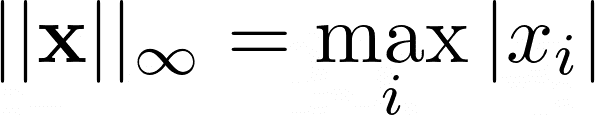
It’s pretty easy to confirm that each one of those norms fulfill the properties of norms listed earlier.
The linalg module in NumPy has capabilities that we will use to compute norms.
Earlier than we start, let’s initialize a vector:
import numpy as np
vector = np.arange(1,7)
print(vector)
L2 Norm in NumPy
Let’s import the linalg module from NumPy:
The norm() operate to compute each matrix and vector norms. This operate takes in a required parameter – the vector or matrix for which we have to compute the norm. As well as, it takes within the following optionally available parameters:
ordthat decides the order of the norm computed, andaxisthat specifies the axis alongside which the norm is to be computed.
After we don’t specify the ord within the operate name, the norm() operate computes the L2 norm by default:
l2_norm = linalg.norm(vector)
print(f"{l2_norm = :.2f}")
We are able to confirm this by explicitly setting ord to 2:
l2_norm = linalg.norm(vector, ord=2)
print(f"{l2_norm = :.2f}")
L1 Norm in NumPy
To calculate the L1 norm of the vector, name the norm() operate with ord = 1:
l1_norm = linalg.norm(vector, ord=1)
print(f"{l1_norm = :.2f}")
Output >> l1_norm = 21.00
As our examples vector accommodates solely optimistic numbers, we will confirm that L1 norm on this case is the same as the sum of the weather:
assert sum(vector) == l1_norm
L∞ Norm in NumPy
To compute the L∞ norm, set ord to ‘np.inf’:
inf_norm = linalg.norm(vector, ord=np.inf)
print(f"{inf_norm = }")
On this instance, we get 6, the most component (within the absolute sense) within the vector:
Within the norm() operate, you may also set ord to ‘-np.inf’.
neg_inf_norm = linalg.norm(vector, ord=-np.inf)
print(f"{neg_inf_norm = }")
As you might have guessed, damaging L∞ norm returns the minimal component (within the absolute sense) within the vector:
Output >> neg_inf_norm = 1.0
A Be aware on L0 Norm
The L0 norm provides the variety of non-zero components within the vector. Technically, it’s not a norm. Reasonably it’s a pseudo norm on condition that it violates the property ||αx|| = |α| ||x||. It’s because the variety of non-zero components stays the identical even when the vector is multiplied by a scalar.
To get the variety of non-zero components in a vector, set ord to 0:
another_vector = np.array([1,2,0,5,0])
l0_norm = linalg.norm(another_vector,ord=0)
print(f"{l0_norm = }")
Right here, another_vector has 3 non-zero components:
Thus far we’ve seen methods to compute vector norms. Simply the best way you possibly can consider vector norms as mappings from an n-dimensional vector area onto the set of actual numbers, matrix norms are a mapping from an m x n matrix area to the set of actual numbers. Mathematically, you possibly can signify this as:

Widespread matrix norms embody the Frobenius and nuclear norms.
Frobenius Norm
For an m x n matrix A with m rows and n columns, the Frobenius norm is given by:
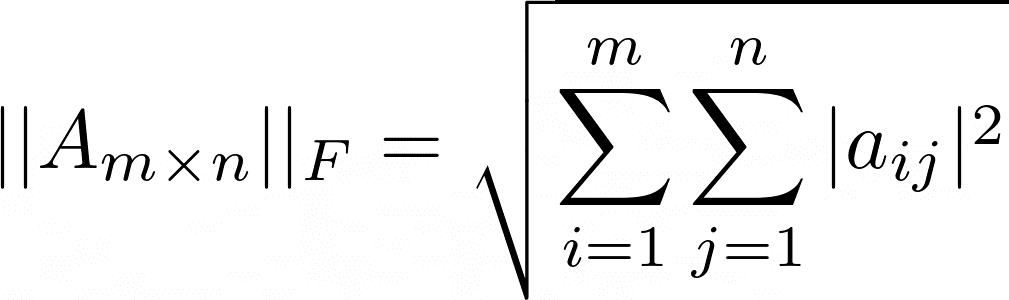
Nuclear Norm
Singular worth decomposition or SVD is a matrix factorization approach utilized in purposes similar to matter modeling, picture compression, and collaborative filtering.
SVD factorizes an enter matrix right into a matrix of a matrix of left singular vectors (U), a matrix of singular values (S), and a matrix of proper singular vectors (V_T). And the nuclear norm is the biggest singular worth of the matrix.

To proceed our dialogue on computing matrix norms in NumPy, let’s reshape vector to a 2 x 3 matrix:
matrix = vector.reshape(2,3)
print(matrix)
Output >>
[[1 2 3]
[4 5 6]]
Matrix Frobenius Norm in NumPy
If you don’t specify the ord parameter, the norm() operate, by default, calculates the Frobenius norm.
Let’s confirm this by setting ord to 'fro':
frob_norm = linalg.norm(matrix,ord='fro')
print(f"{frob_norm = :.2f}")
Output >> frob_norm = 9.54
After we don’t move within the optionally available ord parameter, we get the Frobenius norm, too:
frob_norm = linalg.norm(matrix)
print(f"{frob_norm = :.2f}")
Output >> frob_norm = 9.54
To sum up, when the norm() operate is named with a matrix because the enter, it returns the Frobenius norm of the matrix by default.
Matrix Nuclear Norm in NumPy
To calculate the nuclear norm of a matrix, you possibly can move within the matrix and set ord to ‘nuc’ within the norm() operate name:
nuc_norm = linalg.norm(matrix,ord='nuc')
print(f"{nuc_norm = :.2f}")
Output >> nuc_norm = 10.28
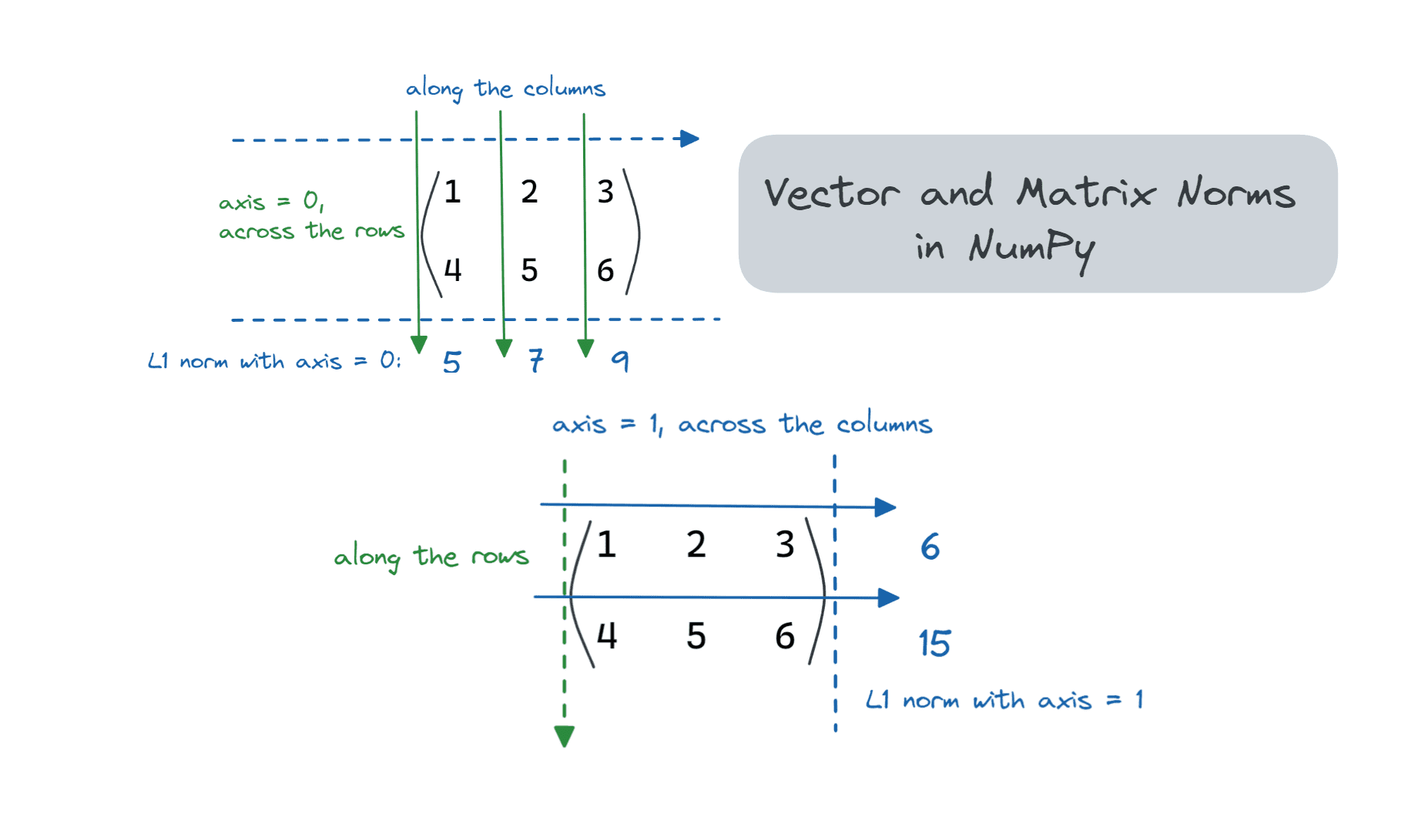
Matrix Norms Alongside a Particular Axis
We typically don’t compute L1 and L2 norms on matrices, however NumPy enables you to compute norms of any ord on matrices (2D-arrays) and different multi-dimensional arrays.
Let’s see methods to compute the L1 norm of a matrix alongside a selected axis – alongside the rows and columns.
Equally, we will set axis = 1.
axis = 0 denotes the rows of a matrix. Should you set axis = 0, the L1 norm of the matrix is calculated throughout the rows (or alongside the columns), as proven:
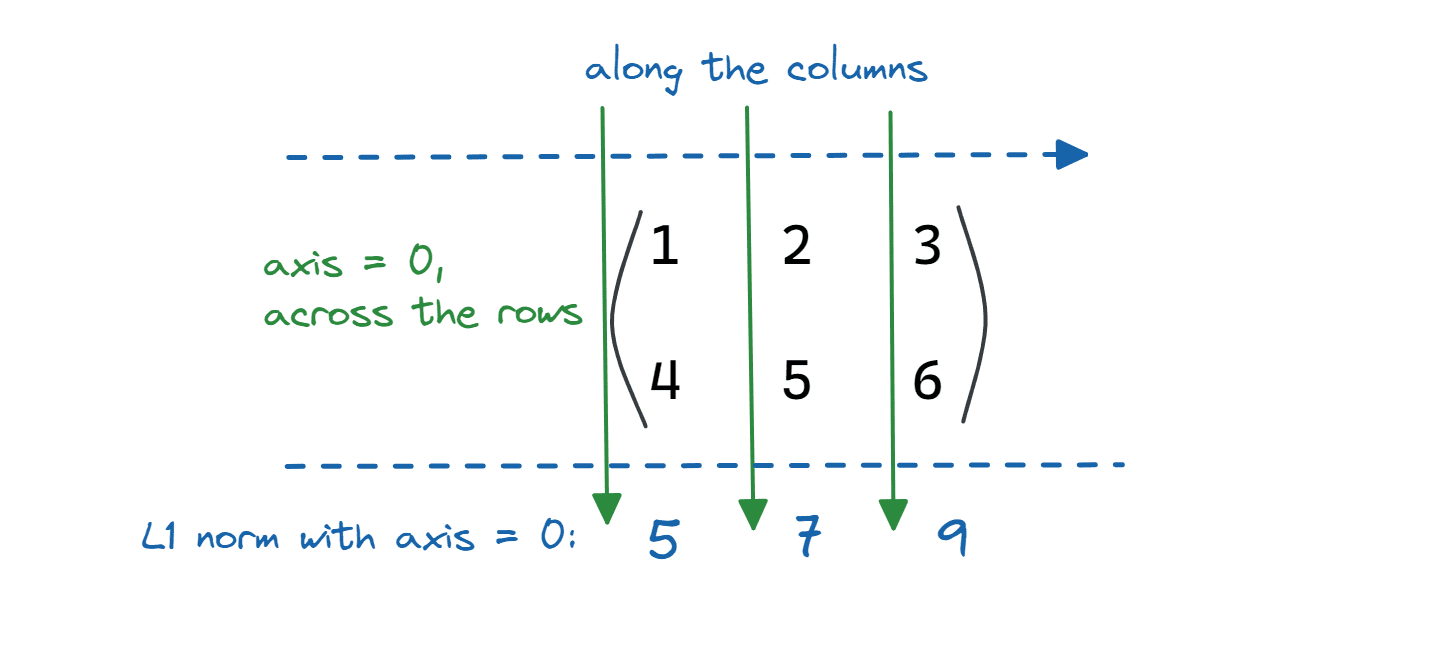
Picture by Writer
Let’s confirm this in NumPy:
matrix_1_norm = linalg.norm(matrix,ord=1,axis=0)
print(f"{matrix_1_norm = }")
Output >> matrix_1_norm = array([5., 7., 9.])
Equally, we will set axis = 1.
axis = 1 denotes the columns of a matrix. So the computation of the L1 norm of the matrix by setting axis = 1 is throughout the columns (alongside the rows).
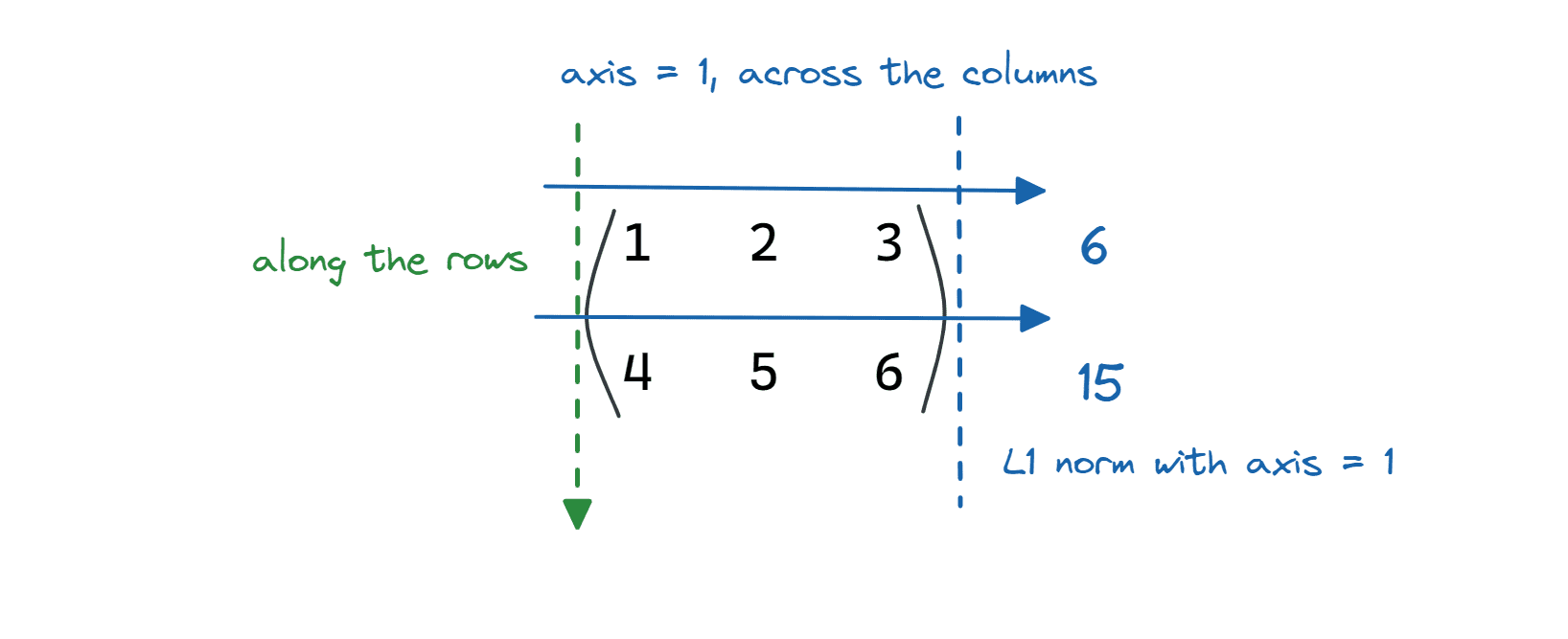
Picture by Writer
matrix_1_norm = linalg.norm(matrix,ord=1,axis=1)
print(f"{matrix_1_norm = }")
Output >> matrix_1_norm = array([ 6., 15.])
I counsel that you simply mess around with the ord and axis parameters on and take a look at with totally different matrices till you get the grasp of it.
I hope you now perceive methods to compute vector and matrix norms utilizing NumPy. It’s essential, nonetheless, to notice that the Frobenius and nuclear norms are outlined just for matrices. So if you happen to attempt computing these norms for vectors or two dimensional arrays and are usually not outlined for elements and or multi-dimensional arrays with greater than two dimensions, you’ll run into errors. That is all for this tutorial!
Bala Priya C is a technical author who enjoys creating long-form content material. Her areas of curiosity embody math, programming, and information science. She shares her studying with the developer neighborhood by authoring tutorials, how-to guides, and extra.





