My Life Stats: I Tracked My Habits for a Yr, and This Is What I Realized | by Pau Blasco i Roca | Nov, 2023
I first appeared on the particular person time collection for 4 variables: Sleep, Learning, Socializing and Temper. I used Microsoft Excel to rapidly draw some plots. They signify the every day variety of hours spent (blue) and the transferring average¹ for 5 days MA(5) (purple) which I thought-about to be a very good measure for my scenario. The temper variable was rated from 10 (the best!) to 0 (terrible!).
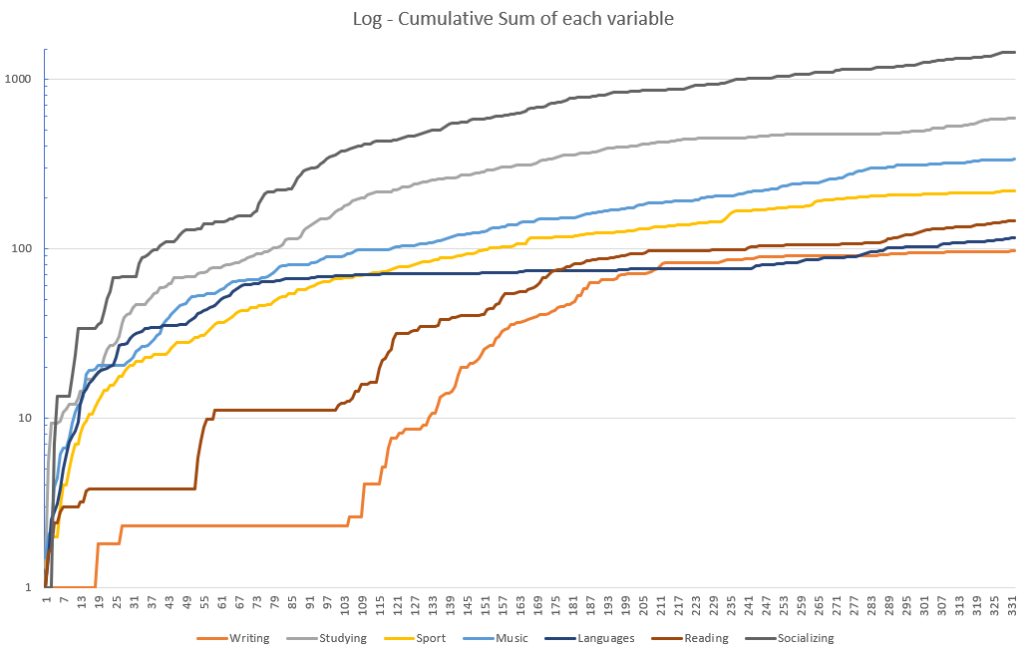
Concerning the information contained within the footnote of every plot: the whole is the sum of the values of the collection, the imply is the arithmetic imply of the collection, the STD is the usual deviation and the relative deviation is the STD divided by the imply.
All issues accounted for, I did nicely sufficient with sleep. I had tough days, like everybody else, however I believe the development is fairly secure. The truth is, it is among the least-varying of my research.
These are the hours I devoted to my tutorial profession. It fluctuates lots — discovering steadiness between work and learning typically means having to cram initiatives on the weekends — however nonetheless, I contemplate myself happy with it.
Concerning this desk, all I can say is that I’m shocked. The grand whole is bigger than I anticipated, on condition that I’m an introvert. In fact, hours with my colleagues at school additionally depend. When it comes to variability, the STD is actually excessive, which is sensible given the problem of getting a stablished routine concerning socializing.
This the least variable collection — the relative deviation is the bottom amongst my studied variables. A priori, I’m happy with the noticed development. I believe it’s constructive to maintain a reasonably secure temper — and even higher if it’s a very good one.
After trying on the traits for the principle variables, I made a decision to dive deeper and research the potential correlations² between them. Since my objective was with the ability to mathematically mannequin and predict (or at the least clarify) “Temper”, correlations have been an vital metric to think about. From them, I might extract relationships like the next: “the times that I research probably the most are those that I sleep the least”, “I normally research languages and music collectively”, and so on.
Earlier than we do the rest, let’s open up a python file and import some key libraries from collection evaluation. I usually use aliases for them, as it’s a widespread follow and makes issues much less verbose within the precise code.
import pandas as pd #1.4.4
import numpy as np #1.22.4
import seaborn as sns #0.12.0
import matplotlib.pyplot as plt #3.5.2
from pmdarima import arima #2.0.4
We’ll make two totally different research concerning correlation. We’ll look into the Particular person Correlation Coefficient³ (for linear relationships between variables) and the Spearman Correlation Coefficient⁴ (which research monotonic relationships between variables). We will likely be utilizing their implementation⁵ in pandas.
Pearson Correlation matrix
The Pearson Correlation Coefficient between two variables X and Y is computed as follows:
We will rapidly calculate a correlation matrix, the place each doable pairwise correlation is computed.
#learn, choose and normalize the information
uncooked = pd.read_csv("final_stats.csv", sep=";")
numerics = uncooked.select_dtypes('quantity')#compute the correlation matrix
corr = numerics.corr(technique='pearson')
#generate the heatmap
sns.heatmap(corr, annot=True)
#draw the plot
plt.present()
That is the uncooked Pearson Correlation matrix obtained from my information.
And these are the numerous values⁶ — those which can be, with a 95% confidence, totally different from zero. We carry out a t-test⁷ with the next formulation. For every correlation worth rho, we discard it if:
the place n is the pattern measurement. We will recycle the code from earlier than and add on this filter.
#constants
N=332 #variety of samples
STEST = 2/np.sqrt(N)def significance_pearson(val):
if np.abs(val)<STEST:
return True
return False
#learn information
uncooked = pd.read_csv("final_stats.csv", sep=";")
numerics = uncooked.select_dtypes('quantity')
#calculate correlation
corr = numerics.corr(technique='pearson')
#put together masks
masks = corr.copy().applymap(significance_pearson)
mask2 = np.triu(np.ones_like(corr, dtype=bool)) #take away higher triangle
mask_comb = np.logical_or(masks, mask2)
c = sns.heatmap(corr, annot=True, masks=mask_comb)
c.set_xticklabels(c.get_xticklabels(), rotation=-45)
plt.present()
These which have been discarded might simply be noise, and wrongfully signify traits or relationships. In any case, it’s higher to imagine a real relationship is meaningless than contemplate significant one which isn’t (what we discuss with as error kind II being favored over error kind I). That is very true in a research with quite subjective measurments.
Spearman’s rank correlation coefficient
The spearman correlation coefficient will be calculated as follows:
As we did earlier than, we are able to rapidly compute the correlation matrix:
#learn, choose and normalize the information
uncooked = pd.read_csv("final_stats.csv", sep=";")
numerics = uncooked.select_dtypes('quantity')#compute the correlation matrix
corr = numerics.corr(technique='spearman') #take note of this modification!
#generate the heatmap
sns.heatmap(corr, annot=True)
#draw the plot
plt.present()
That is the uncooked Spearman’s Rank Correlation matrix obtained from my information:
Let’s see what values are literally important. The formulation to examine for significance is the next:
Right here, we are going to filter out all t-values larger (in absolute worth) than 1.96. Once more, the explanation they’ve been discarded is that we aren’t positive whether or not they’re noise — random probability — or an precise development. Let’s code it up:
#constants
N=332 #variety of samples
TTEST = 1.96def significance_spearman(val):
if val==1:
return True
t = val * np.sqrt((N-2)/(1-val*val))
if np.abs(t)<1.96:
return True
return False
#learn information
uncooked = pd.read_csv("final_stats.csv", sep=";")
numerics = uncooked.select_dtypes('quantity')
#calculate correlation
corr = numerics.corr(technique='spearman')
#put together masks
masks = corr.copy().applymap(significance_spearman)
mask2 = np.triu(np.ones_like(corr, dtype=bool)) #take away higher triangle
mask_comb = np.logical_or(masks, mask2)
#plot the outcomes
c = sns.heatmap(corr, annot=True, masks=mask_comb)
c.set_xticklabels(c.get_xticklabels(), rotation=-45)
plt.present()
These are the numerous values.
I consider this chart higher explains the obvious relationships between variables, as its criterion is extra “pure” (it considers monotonic⁹, and never solely linear, features and relationships). It’s not as impacted by outliers as the opposite one (a few very dangerous days associated to a sure variable received’t impression the general correlation coefficient).
Nonetheless, I’ll go away each charts for the reader to evaluate and extract their very own conclusions.




