Hidden Markov Fashions Defined with a Actual Life Instance and Python code | by Carolina Bento | Nov, 2023
The true world is filled with phenomena for which we are able to see the ultimate end result, however can’t truly observe the underlying elements that generated these outcomes. One instance is predicting the climate, figuring out if it’s going to be wet or sunny tomorrow, primarily based on previous climate observations and the noticed chances of the totally different climate outcomes.
Though pushed by elements we are able to’t observe, with an Hidden Markov Mannequin it’s attainable to mannequin these phenomena as probabilistic programs.
Hidden Markov Models, generally known as HMM for brief, are statistical fashions that work as a sequence of labeling issues. These are the kinds of issues that describe the evolution of observable occasions, which themselves, are depending on inside elements that may’t be instantly noticed — they’re hidden[3].
An Hidden Markov Mannequin is fabricated from two distinct stochastic processes, which means these are processes that may be outlined as sequences of random variables — variables that rely on random occasions.
There’s an invisible course of and an observable course of.
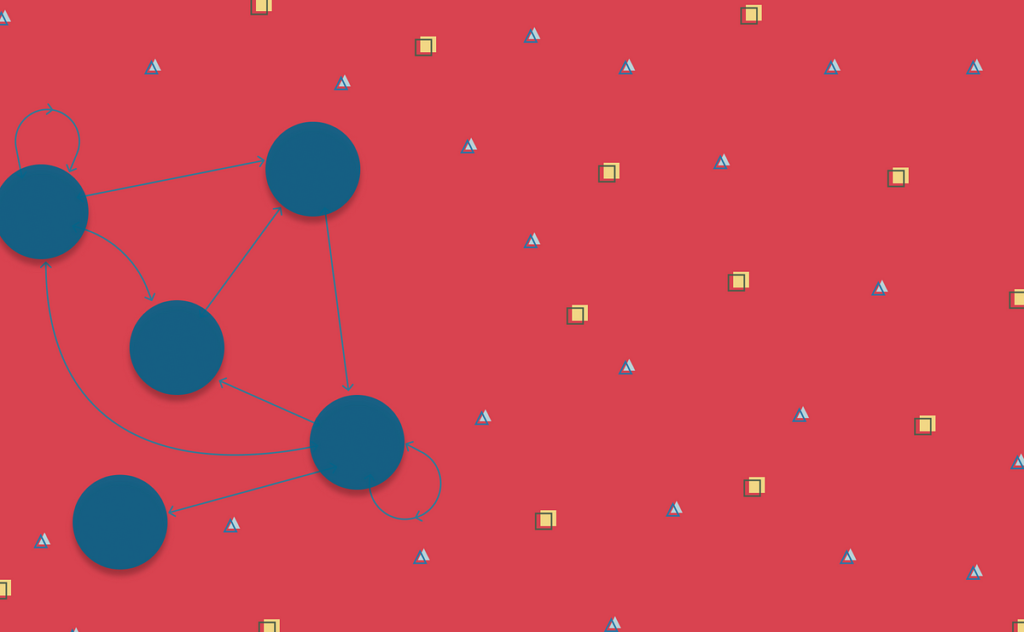
The invisible course of is a Markov Chain, like chaining collectively a number of hidden states which are traversed over time in an effort to attain an end result. This can be a probabilistic course of as a result of all of the parameters of the Markov Chain, in addition to the rating of every sequence, are in reality chances[4].
Hidden Markov Fashions describe the evolution of observable occasions, which themselves, are depending on inside elements that may’t be instantly noticed — they’re hidden[3]
Similar to every other Markov Chain, in an effort to know which state you’re going subsequent, the one factor that issues is the place you at the moment are — through which state of the Markov Chain you’re presently in. Not one of the earlier historical past of states you’ve been previously issues to grasp the place you’re going subsequent.
This sort of short-term reminiscence is among the key traits of HMMs and it’s known as the Markov Assumption, indicating that the chance of reaching the subsequent state is simply depending on the chance of the present state.
The opposite key attribute of an HMM, is that it additionally assumes that every commentary is simply depending on the state that produced it subsequently, being fully unbiased from every other state within the chain[5].
The Markov Assumption states that the chance of reaching the subsequent state is simply depending on the chance of the present state.
That is all nice background info on HMM however, what lessons of issues are they really utilized in?
HMMs assist mannequin the habits of phenomena. Apart from modeling and permitting to run simulations, you can even ask several types of questions these phenomena:
- Probability or Scoring, as in, figuring out the chance of observing a sequence
- Decoding the most effective sequence of states that generated a particular commentary
- Studying the parameters of the HMM that led to observing a given sequence, that traversed a particular set of states.
Let’s have a look at this in follow!
Right this moment you’re not as fearful concerning the climate forecast, what’s in your thoughts is that your canine is probably graduating from their coaching classes. After on a regular basis, effort and canine treats concerned, all you need is for them to succeed.
Throughout canine coaching classes, your four-legged pal is anticipated to do a couple of actions or methods, so the coach can observe and grade their efficiency. After combining the scores of three trials, they’ll decide in case your canine graduates or wants further coaching.
The coach solely sees the result, however there are a number of elements concerned that may’t be instantly noticed comparable to, in case your canine is drained, blissful, in the event that they don’t just like the coach in any respect or the opposite canine round them.
None of those are instantly noticed, until there’s undoubtably a particular motion your canine does solely after they really feel a sure method. Could be nice if they might categorical how they really feel in phrases, perhaps sooner or later!
With Hidden Markov Fashions contemporary in your thoughts, this seems to be like the proper alternative to attempt to predict how your canine was feeling throughout the examination. They could get a sure rating as a result of they had been feeling drained, perhaps they had been hungry, or they had been irritated on the coach.
Your canine has been taking classes for some time and, primarily based on knowledge collected throughout that coaching, you may have all of the constructing blocks wanted to construct a Hidden Markov Mannequin.
With the intention to construct a HMM that fashions the efficiency of your canine within the coaching analysis you want:
- Hidden States
- Transition Matrix
- Sequence of Observations
- Statement Probability Matrix
- Preliminary Chance Distribution
Hidden States are these non-observable elements that affect the commentary sequence. You’ll solely contemplate in case your canine is Drained or Completely satisfied.
Realizing your canine very properly, the non-observable elements that may impression their examination efficiency are merely being drained or blissful.
Subsequent you must know what’s the chance of going from one state to a different, which is captured in a Transition Matrix. This matrix should even be row stochastic which means that the possibilities from one state to every other state within the chain, every row within the matrix, should sum to at least one.
No matter what sort of drawback you’re fixing for, you all the time want a Sequence of Observations. Every commentary representing the results of traversing the Markov Chain. Every commentary is drawn from a particular vocabulary.
Within the case of your canine’s examination you observe the rating they get after every trial, which might be Fail, OK or Good. These are all of the attainable phrases within the commentary vocabulary.
You additionally want the Statement Probability Matrix, which is the chance of an commentary being generated from a particular state.
Lastly, there’s the Preliminary Chance Distribution. That is the chance that the Markov Chain will begin in every particular hidden state.
There will also be some states won’t ever be the beginning state within the Markov Chain. In these conditions, their preliminary chance is zero. And similar to the possibilities within the Transition Matrix, these sum of all preliminary chances should add as much as one.
The Preliminary Chance Distribution, together with the Transition Matrix and the Statement Probability, make up the parameters of an HMM. These are the possibilities you’re determining you probably have a sequence of observations and hidden states, and try to study which particular HMM may have generated them.
Placing all of those items collectively, that is what the Hidden Markov mannequin that represents your canine’s efficiency on the coaching examination seems to be like
Throughout the examination, your canine will carry out three trials, and graduate provided that they don’t Fail in two of these trials.
On the finish of the day, in case your canine wants extra coaching, you’ll take care of all of them the identical. The large query circling your thoughts is How are they feeling throughout the examination.
Imagining a situation the place they graduate with a rating of OK — Fail — Good precisely on this order, what sequence of emotional states will they be in? Will they be principally drained, or hungry all through, or perhaps a mixture of each?
This kind of drawback falls proper beneath the class of Decoding issues that HMMs might be utilized to. On this case, you’re determining what’s the most effective sequence of states that generated a particular sequence of observations, OK — Fail — Good.
The issue of decoding the sequence of states that generated a given sequence of observations leverages the Viterbi Algorithm. Nevertheless, is value doing a brief detour and take a peek into how you would calculate the chance of a given commentary sequence — a Probability job — utilizing the Ahead Algorithm. This can set the stage to raised understanding how the Viterbi Algorithm works.
For those who had been modeling this drawback like a daily Markov Chain, and needed to calculate the probability of observing the sequence of outcomes OK, Fail, Good you’d traverse the chain by touchdown in every particular state that generates the specified end result. At every step you’d take the conditional chance of observing the present end result given that you just’ve noticed the earlier end result and multiply that chance by the transition chance of going from one state to the opposite.
The large distinction is that, in a daily Markov Chain, all states are well-known and observable. Not in an Hidden Markov Mannequin! In an Hidden Markov Mannequin you observe a sequence of outcomes, not figuring out which particular sequence of hidden states needed to be traversed in an effort to observe that.
The large distinction is that, in a daily Markov Chain, all states are well-known and observable. Not in an Hidden Markov Mannequin!
At this level you is likely to be considering, Effectively I can merely traverse all attainable paths and ultimately have a rule to choose between equal paths. The mathematical definition for this method seems to be one thing like this
That’s one technique for certain! You’d should calculate the chance of observing the sequence OK, Fail, Good for each single mixture of hidden states that might ever generate that sequence.
When you may have a sufficiently small variety of hidden states and sequence of noticed outcomes, it is attainable to try this calculation inside an affordable time.
Fortunately, the Hidden Markov mannequin you simply outlined is comparatively easy, with 3 noticed outcomes and a pair of hidden states.
For an noticed sequence of size L outcomes, on a HMM with M hidden states, you may have “M to the facility L” attainable states which in your case, means 2 to the facility of three, i.e., 8 attainable paths for the sequence OK — Fail — Good, involving an exponential computational complexity of O(M^L L), described in Big O-Notation. Because the complexity of the mannequin will increase, the variety of paths you must take into consideration grows exponentially.
Because the complexity of the mannequin will increase, the variety of paths you must take into consideration grows exponentially.
That is the place the Ahead Algorithm shines.
The Ahead Algorithm calculates the chance of a brand new image within the noticed sequence, with out the necessity to calculate the possibilities of all attainable paths that type that sequence [3].
As an alternative of computing the possibilities of all attainable paths that type that sequence the algorithm defines the ahead variable and calculates its worth recursively.
The truth that it makes use of recursion, is the important thing purpose why this algorithm is quicker than calculating all the possibilities of attainable paths. The truth is, it might probably calculate the chance of observing the sequence x in solely “L occasions M squared” computations, as an alternative of “M to the facility of L occasions L”.
In your case, with 2 hidden states and a sequence of three noticed outcomes, it’s the distinction between calculating the possibilities O(MˆL L) = 2³x3 = 8×3 = 24 occasions, versus O(L Mˆ2)=3*2²=3×4 = 12 occasions.
This discount within the variety of calculations is achieved by Dynamic Programming, a programming method that makes use of an auxiliary knowledge constructions to retailer intermediate info, subsequently ensuring the identical calculations aren’t achieved a number of occasions.
Each time the algorithm is about to calculate a brand new chance it checks if it has already computed it, and in that case, it might probably simply entry that worth within the intermediate knowledge construction. In any other case, the chance is calculated and the worth is saved.
Let’s get again to your decoding drawback, utilizing the Viterbi Algorithm.
Considering in pseudo code, For those who had been to brute drive your method into decoding the sequence of hidden states that generate a particular commentary sequence, all you wanted to do was:
- generate all attainable permutations of paths that result in the specified commentary sequence
- use the Ahead Algorithm to calculate the probability of every commentary sequence, for every attainable sequence of hidden states
- decide the sequence of hidden states with highest chance
To your particular HMM, there are 8 attainable paths that result in an end result of OK — Fail — Good. Add only one extra commentary, and also you’ll have double the quantity of attainable sequences of hidden states! Equally to what was described for the Ahead Algorithm, you simply find yourself with an exponentially advanced algorithm and hit efficiency ceiling.
The Viterbi Algorithm, provides you a hand with that.
When the sequence of hidden states within the HMM is traversed, at every step, the chance vt(j) is the chance that the HMM is within the hidden state j after seeing the commentary and is being traversed by way of probably the most possible state that result in j.
The important thing to decoding the sequence of hidden states that generate a particular commentary sequence, is this idea of the most possible path. Additionally known as the Viterbi path, probably the most possible path, is the trail that has highest probability, from all of the paths that may result in any given hidden state.
The important thing to decoding the sequence of hidden states that generate a particular commentary sequence, is to make use of the Viterbi path. Probably the most possible path that results in any given hidden state.
You possibly can draw a parallel between the Ahead Algorithm and the Viterbi Algorithm. The place the Ahead Algorithm sums all chances to acquire the probability of reaching a sure state considering all of the paths that lead there, the Viterbi algorithm doesn’t need to discover all prospects. It focuses on probably the most possible path that results in any given state.
Going again to the duty of decoding the sequence of hidden states that result in the scores of OK — Fail — Good of their examination, working the Viterbi Algorithm by hand would appear to be this
One other distinctive attribute of the Viterbi algorithm is that it should have a option to maintain observe of all of the paths that led to any given hidden state, in an effort to evaluate their chances. To do this it retains observe of backpointers to every hidden state, utilizing an auxiliary knowledge construction typical of dynamic programming algorithms. That method it might probably simply entry the chance of any viterbi path traversed previously.
Backpointers are the important thing to determine probably the most possible path that results in an commentary sequence.
Within the instance of your canine’ examination, while you calculate the Viterbi paths v3(Completely satisfied) and v3(Drained), you decide the trail with highest chance and begin going backwards, i.e., backtracking, by way of all of the paths that led to the place you’re.
Doing all of this by hand is time consuming and error inclined. Miss one vital digit and also you may need to begin from scratch and re-check all of your chances!
The excellent news is which you can leverage software program libraries like hmmlearn, and with a couple of traces of code you may decode the sequence of hidden states that result in your canine graduating with OK — Fail — Good within the trials, precisely on this order.
from hmmlearn import hmm
import numpy as np## Half 1. Producing a HMM with particular parameters and simulating the examination
print("Setup HMM mannequin with parameters")
# init_params are the parameters used to initialize the mannequin for coaching
# s -> begin chance
# t -> transition chances
# e -> emission chances
mannequin = hmm.CategoricalHMM(n_components=2, random_state=425, init_params='ste')
# preliminary chances
# chance of beginning within the Drained state = 0
# chance of beginning within the Completely satisfied state = 1
initial_distribution = np.array([0.1, 0.9])
mannequin.startprob_ = initial_distribution
print("Step 1. Full - Outlined Preliminary Distribution")
# transition chances
# drained blissful
# drained 0.4 0.6
# blissful 0.2 0.8
transition_distribution = np.array([[0.4, 0.6], [0.2, 0.8]])
mannequin.transmat_ = transition_distribution
print("Step 2. Full - Outlined Transition Matrix")
# commentary chances
# Fail OK Good
# drained 0.3 0.5 0.2
# blissful 0.1 0.5 0.4
observation_probability_matrix = np.array([[0.3, 0.5, 0.2], [0.1, 0.5, 0.4]])
mannequin.emissionprob_ = observation_probability_matrix
print("Step 3. Full - Outlined Statement Chance Matrix")
# simulate performing 100,000 trials, i.e., aptitude assessments
trials, simulated_states = mannequin.pattern(100000)
# Output a pattern of the simulated trials
# 0 -> Fail
# 1 -> OK
# 2 -> Good
print("nSample of Simulated Trials - Based mostly on Mannequin Parameters")
print(trials[:10])
## Half 2 - Decoding the hidden state sequence that leads
## to an commentary sequence of OK - Fail - Good
# cut up our knowledge into coaching and check units (50/50 cut up)
X_train = trials[:trials.shape[0] // 2]
X_test = trials[trials.shape[0] // 2:]
mannequin.match(X_train)
# the examination had 3 trials and your canine had the next rating: OK, Fail, Good (1, 0 , 2)
exam_observations = [[1, 0, 2]]
predicted_states = mannequin.predict(X=[[1, 0, 2]])
print("Predict the Hidden State Transitions that had been being the examination scores OK, Fail, Good: n 0 -> Drained , "
"1 -> Completely satisfied")
print(predicted_states)
In a couple of seconds you get an output that matches outcomes the calculations you probably did by hand, a lot quick and with a lot much less room for error.
What’s fascinating about Hidden Markov Fashions is how this statistical instrument created within the mid 1960’s [6] is so highly effective and relevant to actual world issues in such distinct areas, from climate forecasting to discovering the subsequent phrase in a sentence.
On this article, you had the possibility to study concerning the totally different parts of an HMM, how they are often utilized to several types of duties, and recognizing the similarities between the Ahead Algorithm and Viterbi Algorithm. Two very comparable algorithms that use dynamic programming to cope with the exponential variety of calculations concerned.
Both doing the calculations by hand or plugging within the parameters into TensorFlow code, hope you loved diving deep into the world of HMMs.
Thanks for studying!
- D. Khiatani and U. Ghose, “Climate forecasting utilizing Hidden Markov Mannequin,” 2017 Worldwide Convention on Computing and Communication Applied sciences for Sensible Nation (IC3TSN), Gurgaon, India, 2017, pp. 220–225, doi: 10.1109/IC3TSN.2017.8284480.
- Noguchi H, Kato R, Hanai T, Matsubara Y, Honda H, Brusic V, Kobayashi T. Hidden Markov model-based prediction of antigenic peptides that work together with MHC class II molecules. J Biosci Bioeng. 2002;94(3):264–70. doi: 10.1263/jbb.94.264. PMID: 16233301.
- Yoon BJ. Hidden Markov Models and their Applications in Biological Sequence Analysis. Curr Genomics. 2009 Sep;10(6):402–15. doi: 10.2174/138920209789177575. PMID: 20190955; PMCID: PMC2766791.
- Eddy, S. What is a hidden Markov model?. Nat Biotechnol 22, 1315–1316 (2004). https://doi.org/10.1038/nbt1004-1315
- Jurafsky, Dan and Martin, James H.. Speech and language processing : an introduction to pure language processing, computational linguistics, and speech recognition. Higher Saddle River, N.J.: Pearson Prentice Corridor, 2009.
- Baum, Leonard E., and Ted Petrie. “Statistical Inference for Probabilistic Functions of Finite State Markov Chains.” The Annals of Mathematical Statistics 37, no. 6 (1966): 1554–63.