Measurement-induced entanglement part transitions in a quantum circuit – Google Analysis Weblog
Quantum mechanics permits many phenomena which are classically unattainable: a quantum particle can exist in a superposition of two states concurrently or be entangled with one other particle, such that something you do to at least one appears to instantaneously additionally have an effect on the opposite, whatever the house between them. However maybe no facet of quantum idea is as placing because the act of measurement. In classical mechanics, a measurement needn’t have an effect on the system being studied. However a measurement on a quantum system can profoundly affect its habits. For instance, when a quantum bit of data, referred to as a qubit, that’s in a superposition of each “0” and “1” is measured, its state will abruptly collapse to one of many two classically allowed states: will probably be both “0” or “1,” however not each. This transition from the quantum to classical worlds appears to be facilitated by the act of measurement. How precisely it happens is likely one of the elementary unanswered questions in physics.
In a big system comprising many qubits, the impact of measurements could cause new phases of quantum data to emerge. Much like how altering parameters equivalent to temperature and stress could cause a part transition in water from liquid to strong, tuning the energy of measurements can induce a part transition within the entanglement of qubits.
At this time in “Measurement-induced entanglement and teleportation on a noisy quantum processor”, revealed in Nature, we describe experimental observations of measurement-induced results in a system of 70 qubits on our Sycamore quantum processor. That is, by far, the biggest system wherein such a part transition has been noticed. Moreover, we detected “quantum teleportation” — when a quantum state is transferred from one set of qubits to a different, detectable even when the small print of that state are unknown — which emerged from measurements of a random circuit. We achieved this breakthrough by implementing a number of intelligent “methods” to extra readily see the signatures of measurement-induced results within the system.
Background: Measurement-induced entanglement
Think about a system of qubits that begin out unbiased and unentangled with each other. In the event that they work together with each other , they may grow to be entangled. You’ll be able to think about this as an internet, the place the strands symbolize the entanglement between qubits. As time progresses, this net grows bigger and extra intricate, connecting more and more disparate factors collectively.
A full measurement of the system utterly destroys this net, since each entangled superposition of qubits collapses when it’s measured. However what occurs once we make a measurement on just a few of the qubits? Or if we wait a very long time between measurements? Through the period in-between, entanglement continues to develop. The online’s strands might not lengthen as vastly as earlier than, however there are nonetheless patterns within the net.
There’s a balancing level between the energy of interactions and measurements, which compete to have an effect on the intricacy of the online. When interactions are sturdy and measurements are weak, entanglement stays sturdy and the online’s strands lengthen farther, however when measurements start to dominate, the entanglement net is destroyed. We name the crossover between these two extremes the measurement-induced part transition.
In our quantum processor, we observe this measurement-induced part transition by various the relative strengths between interactions and measurement. We induce interactions by performing entangling operations on pairs of qubits. However to truly see this net of entanglement in an experiment is notoriously difficult. First, we will by no means truly have a look at the strands connecting the qubits — we will solely infer their existence by seeing statistical correlations between the measurement outcomes of the qubits. So, we have to repeat the identical experiment many occasions to deduce the sample of the online. However there’s one other complication: the online sample is completely different for every doable measurement end result. Merely averaging the entire experiments collectively with out regard for his or her measurement outcomes would wash out the webs’ patterns. To handle this, some earlier experiments used “post-selection,” the place solely knowledge with a specific measurement end result is used and the remaining is thrown away. This, nonetheless, causes an exponentially decaying bottleneck within the quantity of “usable” knowledge you possibly can purchase. As well as, there are additionally sensible challenges associated to the problem of mid-circuit measurements with superconducting qubits and the presence of noise within the system.
How we did it
To handle these challenges, we launched three novel methods to the experiment that enabled us to look at measurement-induced dynamics in a system of as much as 70 qubits.
Trick 1: House and time are interchangeable
As counterintuitive as it could appear, interchanging the roles of house and time dramatically reduces the technical challenges of the experiment. Earlier than this “space-time duality” transformation, we’d have needed to interleave measurements with different entangling operations, continuously checking the state of chosen qubits. As an alternative, after the transformation, we will postpone all measurements till in any case different operations, which enormously simplifies the experiment. As applied right here, this transformation turns the unique 1-spatial-dimensional circuit we have been all for finding out right into a 2-dimensional one. Moreover, since all measurements at the moment are on the finish of the circuit, the relative energy of measurements and entangling interactions is tuned by various the variety of entangling operations carried out within the circuit.
Trick 2: Overcoming the post-selection bottleneck
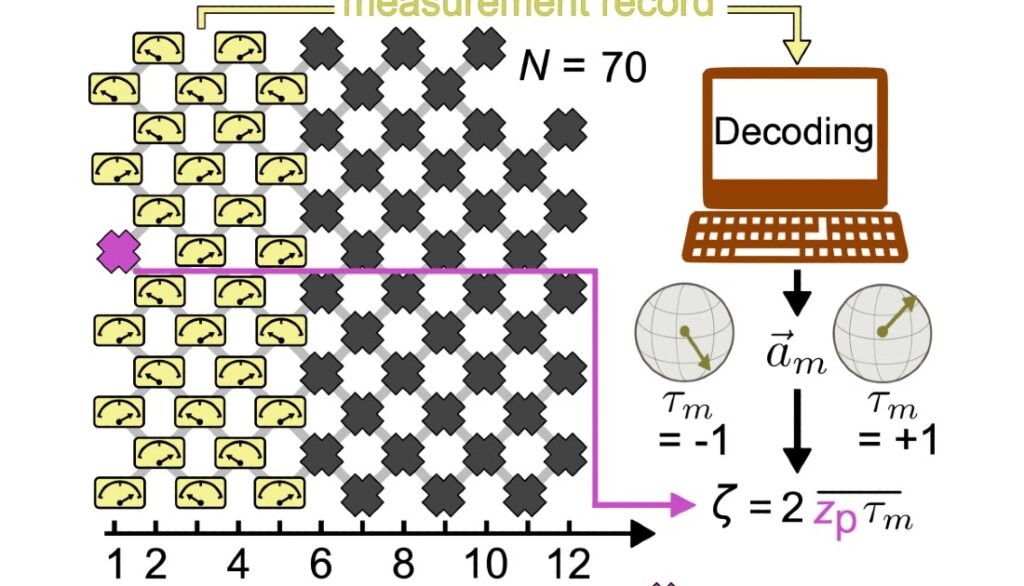
Since every mixture of measurement outcomes on the entire qubits leads to a singular net sample of entanglement, researchers typically use post-selection to look at the small print of a specific net. Nevertheless, as a result of this methodology could be very inefficient, we developed a brand new “decoding” protocol that compares every occasion of the actual “net” of entanglement to the identical occasion in a classical simulation. This avoids post-selection and is delicate to options which are frequent to the entire webs. This frequent characteristic manifests itself right into a mixed classical–quantum “order parameter”, akin to the cross-entropy benchmark used within the random circuit sampling utilized in our beyond-classical demonstration.
This order parameter is calculated by choosing one of many qubits within the system because the “probe” qubit, measuring it, after which utilizing the measurement report of the close by qubits to classically “decode” what the state of the probe qubit must be. By cross-correlating the measured state of the probe with this “decoded” prediction, we will receive the entanglement between the probe qubit and the remainder of the (unmeasured) qubits. This serves as an order parameter, which is a proxy for figuring out the entanglement traits of your entire net.
Trick 3: Utilizing noise to our benefit
A key characteristic of the so-called “disentangling part” — the place measurements dominate and entanglement is much less widespread — is its insensitivity to noise. We will subsequently have a look at how the probe qubit is affected by noise within the system and use that to distinguish between the 2 phases. Within the disentangling part, the probe will likely be delicate solely to native noise that happens inside a specific space close to the probe. However, within the entangling part, any noise within the system can have an effect on the probe qubit. On this means, we’re turning one thing that’s usually seen as a nuisance in experiments into a singular probe of the system.
What we noticed
We first studied how the order parameter was affected by noise in every of the 2 phases. Since every of the qubits is noisy, including extra qubits to the system provides extra noise. Remarkably, we certainly discovered that within the disentangling part the order parameter is unaffected by including extra qubits to the system. It’s because, on this part, the strands of the online are very brief, so the probe qubit is just delicate to the noise of its nearest qubits. In distinction, we discovered that within the entangling part, the place the strands of the entanglement net stretch longer, the order parameter could be very delicate to the scale of the system, or equivalently, the quantity of noise within the system. The transition between these two sharply contrasting behaviors signifies a transition within the entanglement character of the system because the “energy” of measurement is elevated.
In our experiment, we additionally demonstrated a novel type of quantum teleportation that arises within the entangling part. Sometimes, a selected set of operations are essential to implement quantum teleportation, however right here, the teleportation emerges from the randomness of the non-unitary dynamics. When all qubits, besides the probe and one other system of distant qubits, are measured, the remaining two methods are strongly entangled with one another. With out measurement, these two methods of qubits can be too distant from one another to know in regards to the existence of one another. With measurements, nonetheless, entanglement could be generated sooner than the boundaries sometimes imposed by locality and causality. This “measurement-induced entanglement” between the qubits (that should even be aided with a classical communications channel) is what permits for quantum teleportation to happen.
Conclusion
Our experiments display the impact of measurements on a quantum circuit. We present that by tuning the energy of measurements, we will induce transitions to new phases of quantum entanglement inside the system and even generate an emergent type of quantum teleportation. This work might doubtlessly have relevance to quantum computing schemes, the place entanglement and measurements each play a job.
Acknowledgements
This work was accomplished whereas Jesse Hoke was interning at Google from Stanford College. We wish to thank Katie McCormick, our Quantum Science Communicator, for serving to to write down this weblog publish.