Simplifying Transformers: State of the Artwork NLP Utilizing Phrases You Perceive — half 3— Consideration | by Chen Margalit | Aug, 2023
Tansformers have made a critical impression within the subject of AI, maybe in the complete world. This structure is comprised of a number of parts, however as the unique paper is called “Consideration is All You Want”, it’s considerably evident that the eye mechanism holds specific significance. Half 3 of this sequence will primarily consider consideration and the functionalities round it that be certain the Transformer philharmonic performs nicely collectively.
Consideration
Within the context of Transformers, consideration refers to a mechanism that permits the mannequin to concentrate on related components of the enter throughout processing. Picture a flashlight that shines on particular components of a sentence, permitting the mannequin to present extra to much less significance relying on context. I imagine examples are more practical than definitions as a result of they’re some form of mind teaser, offering the mind with the likelihood to bridge the gaps and comprehend the idea by itself.
When introduced with the sentence, “The person took the chair and disappeared,” you naturally assign various levels of significance (e.g. consideration) to totally different components of the sentence. Considerably surprisingly, if we take away particular phrases, the which means stays principally intact: “man took chair disappeared.” Though this model is damaged English, in comparison with the unique sentence you possibly can nonetheless perceive the essence of the message. Curiously, three phrases (“The,” “the,” and “and”) account for 43% of the phrases within the sentence however don’t contribute considerably to the general which means. This statement was most likely clear to each Berliner who got here throughout my wonderful German whereas residing there (one can both study German or be completely satisfied, it is a determination you must make) but it surely’s a lot much less obvious to ML fashions.
Up to now, earlier architectures like RNNs, (Recurrent Neural Networks) confronted a major problem: they struggled to “bear in mind” phrases that appeared far again within the enter sequence, usually past 20 phrases. As you already know, these fashions basically depend on mathematical operations to course of knowledge. Sadly, the mathematical operations utilized in earlier architectures weren’t environment friendly sufficient to hold phrase representations adequately into the distant way forward for the sequence.
This limitation in long-term dependency hindered the flexibility of RNNs to keep up contextual info over prolonged intervals, impacting duties resembling language translation or sentiment evaluation the place understanding the complete enter sequence is essential. Nonetheless, Transformers, with their consideration mechanism and self-attention mechanisms, deal with this subject extra successfully. They’ll effectively seize dependencies throughout lengthy distances within the enter, enabling the mannequin to retain context and associations even for phrases that seem a lot earlier within the sequence. In consequence, Transformers have develop into a groundbreaking resolution to beat the restrictions of earlier architectures and have considerably improved the efficiency of assorted pure language processing duties.
To create distinctive merchandise just like the superior chatbots we encounter right now, it’s important to equip the mannequin with the flexibility to differentiate between excessive and low-value phrases and in addition retain contextual info over lengthy distances within the enter. The mechanism launched within the Transformers structure to deal with these challenges is named consideration.
*People have been growing methods to discriminate between people for a really very long time, however as inspiring as they’re, we gained’t be utilizing these right here.
Dot Product
How can a mannequin even theoretically discern the significance of various phrases? When analyzing a sentence, we goal to establish the phrases which have stronger relationships with each other. As phrases are represented as vectors (of numbers), we’d like a measurement for the similarity between numbers. The mathematical time period for measuring vector similarity is “Dot Product.” It includes multiplying parts of two vectors and producing a scalar worth (e.g., 2, 16, -4.43), which serves as a illustration of their similarity. Machine Studying is grounded in varied mathematical operations, and amongst them, the Dot Product holds specific significance. Therefore, I’ll take the time to elaborate on this idea.
Instinct
Picture we now have actual representations (embeddings) for five phrases: “florida”, “california”, “texas”, “politics” and “fact”. As embeddings are simply numbers, we will probably plot them on a graph. Nonetheless, resulting from their excessive dimensionality (the variety of numbers used to characterize the phrase), which may simply vary from 100 to 1000, we will’t actually plot them as they’re. We will’t plot a 100-dimensional vector on a 2D pc/cellphone display. Furthermore, The human mind finds it obscure one thing above 3 dimensions. What does a four-dimensional vector appear like? I don’t know.
To beat this subject, we make the most of Principal Element Evaluation (PCA), a method that reduces the variety of dimensions. By making use of PCA, we will challenge the embeddings onto a 2-dimensional area (x,y coordinates). This discount in dimensions helps us visualize the info on a graph. Though we lose some info because of the discount, hopefully, these diminished vectors will nonetheless protect sufficient similarities to the unique embeddings, enabling us to achieve insights and comprehend relationships among the many phrases.
These numbers are primarily based on the GloVe Embeddings.
florida = [-2.40062016, 0.00478901]
california = [-2.54245794, -0.37579669]
texas = [-2.24764634, -0.12963368]
politics = [3.02004564, 2.88826688]
fact = [4.17067881, -2.38762552]
You possibly can maybe discover there’s some sample within the numbers, however we’ll plot the numbers to make life simpler.
On this visualization, we see 5 2D vectors (x,y coordinates), representing 5 totally different phrases. As you possibly can see, the plot suggests some phrases are way more associated to others.
math
The mathematical counterpart of visualizing vectors will be expressed by way of an easy equation. When you aren’t significantly keen on arithmetic and recall the authors’ description of the Transformers structure as a “easy community structure,” you most likely assume that is what occurs to ML individuals, they get bizarre. It is most likely true, however not on this case, this is easy. I’ll clarify:
The image ||a|| denotes the magnitude of vector “a,” which represents the space between the origin (level 0,0) and the tip of the vector. The calculation for the magnitude is as follows:
The end result of this calculation is a quantity, resembling 4, or 12.4.
Theta (θ), refers back to the angle between the vectors (have a look at the visualization). The cosine of theta, denoted as cos(θ), is solely the results of making use of the cosine operate to that angle.
code
Utilizing the GloVe algorithm, researchers from Stanford College have generated embeddings for precise phrases, as we mentioned earlier. Though they’ve their particular approach for creating these embeddings, the underlying idea stays the identical as we talked about in the previous part of the series. For instance, I took 4 phrases, diminished their dimensionality to 2, after which plotted their vectors as easy x and y coordinates.
To make this course of operate appropriately, downloading the GloVe embeddings is a crucial prerequisite.
*A part of the code, particularly the primary field is impressed by some code I’ve seen, however I can’t appear to search out the supply.
import pandas as pdpath_to_glove_embds = 'glove.6B.100d.txt'
glove = pd.read_csv(path_to_glove_embds, sep=" ", header=None, index_col=0)
glove_embedding = {key: val.values for key, val in glove.T.gadgets()}
phrases = ['florida', 'california', 'texas', 'politics', 'truth']
word_embeddings = [glove_embedding[word] for phrase in phrases]print(word_embeddings[0]).form # 100 numbers to characterize every phrase.
---------------------
output:
(100,)
pca = PCA(n_components=2) # cut back dimensionality from 100 to 2.
word_embeddings_pca = pca.fit_transform(word_embeddings)
for i in vary(5):
print(word_embeddings_pca[i])---------------------
output:
[-2.40062016 0.00478901] # florida
[-2.54245794 -0.37579669] # california
[-2.24764634 -0.12963368] # texas
[3.02004564 2.88826688] # politics
[ 4.17067881 -2.38762552] # fact
We now possess a real illustration of all 5 phrases. Our subsequent step is to conduct the dot product calculations.
Vector magnitude:
import numpy as npflorida_vector = [-2.40062016, 0.00478901]
florida_vector_magnitude = np.linalg.norm(florida_vector)
print(florida_vector_magnitude)
---------------------
output:
2.4006249368060817 # The magnitude of the vector "florida" is 2.4.
Dot Product between two related vectors.
import numpy as npflorida_vector = [-2.40062016, 0.00478901]
texas_vector = [-2.24764634 -0.12963368]
print(np.dot(florida_vector, texas_vector))
---------------------
output:
5.395124299364358
Dot Product between two dissimilar vectors.
import numpy as npflorida_vector = [-2.40062016, 0.00478901]
truth_vector = [4.17067881, -2.38762552]
print(np.dot(florida_vector, truth_vector))
---------------------
output:
-10.023649994662344
As evident from the dot product calculation, it seems to seize and replicate an understanding of similarities between totally different ideas.
Scaled Dot-Product consideration
instinct
Now that we now have a grasp of Dot Product, we will delve again into consideration. Notably, the self-attention mechanism. Utilizing self-attention gives the mannequin with the flexibility to find out the significance of every phrase, no matter its “bodily” proximity to the phrase. This allows the mannequin to make knowledgeable selections primarily based on the contextual relevance of every phrase, main to higher understanding.
To attain this formidable objective, we create 3 matrics composed out of learnable (!) parameters, often called Question, Key and Worth (Q, Ok, V). The question matrix will be envisioned as a question matrix containing the phrases the person inquires or asks for (e.g. once you ask chatGPT if: “god is accessible right now at 5 p.m.?” that’s the question). The Key matrix encompasses all different phrases within the sequence. By computing the dot product between these matrices, we get the diploma of relatedness between every phrase and the phrase we’re presently inspecting (e.g., translating, or producing the reply to the question).
The Worth Matrix gives the “clear” illustration for each phrase within the sequence. Why do I check with it as clear the place the opposite two matrices are shaped in the same method? as a result of the worth matrix stays in its authentic kind, we don’t use it after multiplication by one other matrix or normalize it by some worth. This distinction units the Worth matrix aside, making certain that it preserves the unique embeddings, free from extra computations or transformations.
All 3 matrices are constructed with a measurement of word_embedding (512). Nonetheless, they’re divided into “heads”. Within the paper the authors used 8 heads, leading to every matrix having a measurement of sequence_length by 64. You may surprise why the identical operation is carried out 8 instances with 1/8 of the info and never as soon as with all the info. The rationale behind this strategy is that by conducting the identical operation 8 instances with 8 totally different units of weights (that are as talked about, learnable), we will exploit the inherent range within the knowledge. Every head can concentrate on a selected side throughout the enter and in combination, this could result in higher efficiency.
*In most implementations we do not actually divide the principle matrix to eight. The division is achieved by way of indexing, permitting parallel processing for every half. Nonetheless, these are simply implementation particulars. Theoretically, we might’ve executed just about the identical utilizing 8 matrices.
The Q and Ok are multiplied (dot product) after which normalized by the sq. root of the variety of dimensions. We go the end result by way of a Softmax operate and the result’s then multiplied by the matrix V.
The rationale for normalizing the outcomes is that Q and Ok are matrices which are generated considerably randomly. Their dimensions could be fully unrelated (unbiased) and multiplications between unbiased matrices may lead to very large numbers which may hurt the training as I’ll clarify later on this half.
We then use a non-linear transformation named Softmax, to make all numbers vary between 0 and 1, and sum to 1. The result’s much like a likelihood distribution (as there are numbers from 0 to 1 that add as much as 1). These numbers exemplify the relevance of each phrase to each different phrase within the sequence.
Lastly, we multiply the end result by matrix V, and lo and behold, we’ve received the self-attention rating.
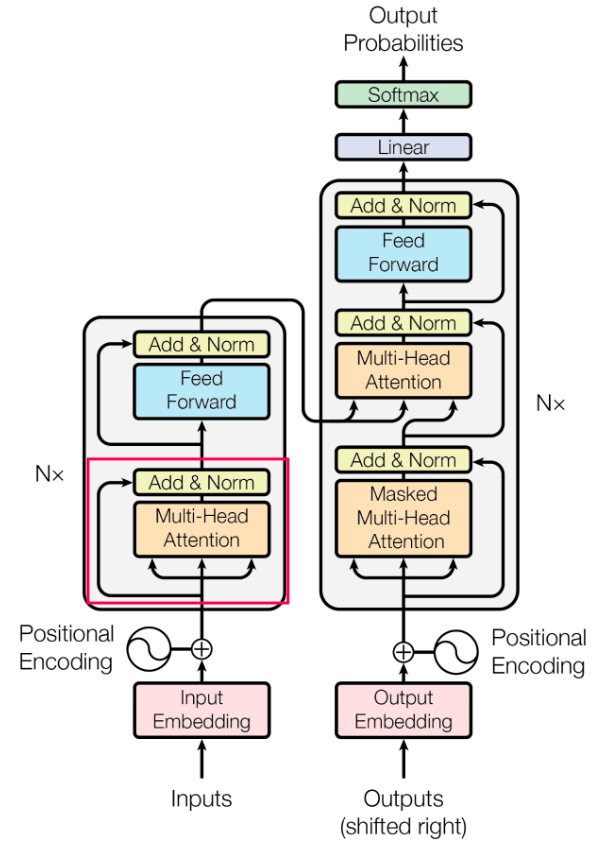
*The encoder is definitely constructed out of N (within the paper, N=6) similar layers, every such layer will get its enter from the earlier layer and does the identical. The ultimate layer passes the info each to the Decoder (which we are going to speak about in a later a part of this sequence) and to the higher layers of the Encoder.
Here’s a visualization of self-attention. It is like teams of pals in a classroom. Some individuals are extra linked to some individuals. Some individuals aren’t very nicely linked to anybody.
math
Thq Q, Ok and V matrices are derived by way of a linear transformation of the embedding matrix. Linear transformations are necessary in machine studying, and if you are interested in turning into an ML practitioner, I like to recommend exploring them additional. I will not delve deep, however I’ll say that linear transformation is a mathematical operation that strikes a vector (or a matrix) from one area to a different area. It sounds extra complicated than it’s. Think about an arrow pointing in a single route, after which shifting to level 30 levels to the appropriate. This illustrates a linear transformation. There are just a few situations for such an operation to be thought of linear but it surely’s probably not necessary for now. The important thing takeaway is that it retains most of the authentic vector properties.
The complete calculation of the self-attention layers is carried out by making use of the next components:
The calculation course of unfolds as follows:
1. We multiply Q by Ok transposed (flipped).
2. We divide the end result by the sq. root of the dimensionality of matrix Ok.
3. We now have the “consideration matrix scores” that describe how related each phrase is to each different phrase. We go each row to a Softmax (a non-linear) transformation. Softmax does three fascinating related issues:
a. It scales all of the numbers so they’re between 0 and 1.
b. It makes all of the numbers sum to 1.
c. It accentuates the gaps, making the marginally extra necessary, way more necessary. In consequence, we will now simply distinguish the various levels to which the mannequin perceives the connection between phrases x1 and x2, x3, x4, and so forth.
4. We multiply the rating by the V matrix. That is the ultimate results of the self-attention operation.
Masking
Within the previous chapter in this series, I’ve defined that we make use of dummy tokens to deal with particular occurrences within the sentence resembling the primary phrase within the sentence, the final phrase, and so forth. One in all these tokens, denoted as <PADDING>, signifies that there isn’t any precise knowledge, and but we have to keep constant matrix sizes all through the complete course of. To make sure the mannequin comprehends these are dummy tokens and may subsequently not be thought of throughout the self-attention calculation, we characterize these tokens as minus infinity (e.g. a really giant unfavorable quantity, e.g. -153513871339). The masking values are added to the results of the multiplication between Q by Ok. Softmax then turns these numbers into 0. This enables us to successfully ignore the dummy tokens throughout the consideration mechanism whereas preserving the integrity of the calculations.
Dropout
Following the self-attention layer, a dropout operation is utilized. Dropout is a regularization approach extensively utilized in Machine Studying. The aim of regularization is to impose constraints on the mannequin throughout coaching, making it harder for the mannequin to rely closely on particular enter particulars. In consequence, the mannequin learns extra robustly and improves its capability to generalize. The precise implementation includes selecting a few of the activations (the numbers popping out of various layers) randomly, and zeroing them out. In each go of the identical layer, totally different activations will probably be zeroed out stopping the mannequin from discovering options which are particular to the info it will get. In essence, dropout helps in enhancing the mannequin’s capability to deal with numerous inputs and making it harder for the mannequin to be tailor-made to particular patterns within the knowledge.
Skip connection
One other necessary operation executed within the Transformer structure known as Skip Connection.
Skip Connection is a solution to go enter with out subjecting it to any transformation. For example, think about that I report back to my supervisor who reviews it to his supervisor. Even with very pure intentions of creating the report extra helpful, the enter now goes by way of some modifications when processed by one other human (or ML layer). On this analogy, the Skip-Connection can be me, reporting straight to my supervisor’s supervisor. Consequently, the higher supervisor receives enter each by way of my supervisor (processed knowledge) and straight from me (unprocessed). The senior supervisor can then hopefully make a greater determination. The rationale behind using skip connections is to deal with potential points resembling vanishing gradients which I’ll clarify within the following part.
Add & Norm Layer
Instinct
The “Add & Norm” layer performs addition and normalization. I’ll begin with addition because it’s easier. Principally, we add the output from the self-attention layer to the unique enter (obtained from the skip connection). This addition is finished element-wise (each quantity to its identical positioned quantity). The result’s then normalized.
The rationale we normalize, once more, is that every layer performs quite a few calculations. Multiplying numbers many instances can result in unintended eventualities. For example, if I take a fraction, like 0.3, and I multiply it with one other fraction, like 0.9, I get 0.27 which is smaller than the place it began. if I do that many instances, I’d find yourself with one thing very near 0. This might result in an issue in deep studying referred to as vanishing gradients.
I gained’t go too deep proper now so this text doesn’t take ages to learn, however the concept is that if numbers develop into very near 0, the mannequin will not be capable to study. The premise of recent ML is calculating gradients and adjusting the weights utilizing these gradients (and some different elements). If these gradients are near 0, it is going to be very troublesome for the mannequin to study successfully.
Quite the opposite, the alternative phenomenon, referred to as exploding gradients, can happen when numbers that aren’t fractions get multiplied by non-fractions, inflicting the values to develop into excessively giant. In consequence, the mannequin faces difficulties in studying because of the monumental modifications in weights and activations, which may result in instability and divergence throughout the coaching course of.
ML fashions are considerably like a small youngster, they want safety. One of many methods to guard these fashions from numbers getting too large or too small is normalization.
Math
The layer normalization operation appears scary (as all the time) but it surely’s truly comparatively easy.
Within the layer normalization operation, we comply with these easy steps for every enter:
- Subtract its imply from the enter.
- Divide by the sq. root of the variance and add an epsilon (some tiny quantity), used to keep away from division by zero.
- Multiply the ensuing rating by a learnable parameter referred to as gamma (γ).
- Add one other learnable parameter referred to as beta (β).
These steps make sure the imply will probably be near 0 and the usual deviation near 1. The normalization course of enhances the coaching’s stability, velocity, and general efficiency.
Code
# x being the enter.(x - imply(x)) / sqrt(variance(x) + epsilon) * gamma + beta
Abstract:
At this level, we now have a stable understanding of the principle inside workings of the Encoder. Moreover, we now have explored Skip Connections, a purely technical (and necessary) approach in ML that improves the mannequin’s capability to study.
Though this part is a bit difficult, you’ve gotten already acquired a considerable understanding of the Transformers structure as a complete. As we progress additional within the sequence, this understanding will serve you in understanding the remaining components.
Keep in mind, that is the State of the Artwork in an advanced subject. This isn’t straightforward stuff. Even in case you nonetheless don’t perceive the whole lot 100%, nicely executed for making this nice progress!
The subsequent half will probably be a couple of foundational (and easier) idea in Machine Studying, the Feed Ahead Neural Community.