An introduction to climate forecasting with deep studying
With all that is occurring on the earth nowadays, is it frivolous to speak about climate prediction? Requested within the twenty first
century, that is certain to be a rhetorical query. Within the Thirties, when German poet Bertolt Brecht wrote the well-known traces:
Was sind das für Zeiten, wo
Ein Gespräch über Bäume quick ein Verbrechen ist
Weil es ein Schweigen über so viele Untaten einschließt!
(“What sort of occasions are these, the place a dialog about timber is nearly a criminal offense, for it means silence about so many
atrocities!”),
he couldn’t have anticipated the responses he would get within the second half of that century, with timber symbolizing, in addition to
actually falling sufferer to, environmental air pollution and local weather change.
Right now, no prolonged justification is required as to why prediction of atmospheric states is important: As a consequence of world warming,
frequency and depth of extreme climate circumstances – droughts, wildfires, hurricanes, heatwaves – have risen and can
proceed to rise. And whereas correct forecasts don’t change these occasions per se, they represent important data in
mitigating their penalties. This goes for atmospheric forecasts on all scales: from so-called “nowcasting” (working on a
vary of about six hours), over medium-range (three to 5 days) and sub-seasonal (weekly/month-to-month), to local weather forecasts
(involved with years and many years). Medium-range forecasts particularly are extraordinarily necessary in acute catastrophe prevention.
This submit will present how deep studying (DL) strategies can be utilized to generate atmospheric forecasts, utilizing a newly revealed
benchmark dataset(Rasp et al. 2020). Future posts could refine the mannequin used right here
and/or talk about the function of DL (“AI”) in mitigating local weather change – and its implications – extra globally.
That mentioned, let’s put the present endeavor in context. In a approach, now we have right here the standard dejà vu of utilizing DL as a
black-box-like, magic instrument on a process the place human information was once required. In fact, this characterization is
overly dichotomizing; many selections are made in creating DL fashions, and efficiency is essentially constrained by out there
algorithms – which can, or could not, match the area to be modeled to a adequate diploma.
Should you’ve began studying about picture recognition fairly not too long ago, it’s possible you’ll nicely have been utilizing DL strategies from the outset,
and never have heard a lot concerning the wealthy set of function engineering strategies developed in pre-DL picture recognition. Within the
context of atmospheric prediction, then, let’s start by asking: How on the earth did they try this earlier than?
Numerical climate prediction in a nutshell
It isn’t like machine studying and/or statistics will not be already utilized in numerical climate prediction – quite the opposite. For
instance, each mannequin has to start out from someplace; however uncooked observations will not be suited to direct use as preliminary circumstances.
As a substitute, they need to be assimilated to the four-dimensional grid over which mannequin computations are carried out. On the
different finish, specifically, mannequin output, statistical post-processing is used to refine the predictions. And really importantly, ensemble
forecasts are employed to find out uncertainty.
That mentioned, the mannequin core, the half that extrapolates into the long run atmospheric circumstances noticed at present, is predicated on a
set of differential equations, the so-called primitive equations,
which are as a result of conservation legal guidelines of momentum,
energy, and
mass. These differential equations can’t be solved analytically;
fairly, they need to be solved numerically, and that on a grid of decision as excessive as attainable. In that mild, even deep
studying may seem as simply “reasonably resource-intensive” (dependent, although, on the mannequin in query). So how, then,
may a DL method look?
Deep studying fashions for climate prediction
Accompanying the benchmark dataset they created, Rasp et al.(Rasp et al. 2020) present a set of notebooks, together with one
demonstrating the usage of a easy convolutional neural community to foretell two of the out there atmospheric variables, 500hPa
geopotential and 850hPa temperature. Right here 850hPa temperature is the (spatially various) temperature at a repair atmospheric
peak of 850hPa (~ 1.5 kms) ; 500hPa geopotential is proportional to the (once more, spatially various) altitude
related to the stress degree in query (500hPa).
For this process, two-dimensional convnets, as often employed in picture processing, are a pure match: Picture width and peak
map to longitude and latitude of the spatial grid, respectively; goal variables seem as channels. On this structure,
the time collection character of the info is basically misplaced: Each pattern stands alone, with out dependency on both previous or
current. On this respect, in addition to given its dimension and ease, the convnet introduced beneath is just a toy mannequin, meant to
introduce the method in addition to the appliance total. It might additionally function a deep studying baseline, together with two
different varieties of baseline generally utilized in numerical climate prediction launched beneath.
Instructions on tips on how to enhance on that baseline are given by current publications. Weyn et al.(Weyn, Durran, and Caruana, n.d.), along with making use of
extra geometrically-adequate spatial preprocessing, use a U-Internet-based structure as a substitute of a plain convnet. Rasp and Thuerey
(Rasp and Thuerey 2020), constructing on a totally convolutional, high-capacity ResNet structure, add a key new procedural ingredient:
pre-training on local weather fashions. With their methodology, they can not simply compete with bodily fashions, but in addition, present
proof of the community studying about bodily construction and dependencies. Sadly, compute services of this order
will not be out there to the typical particular person, which is why we’ll content material ourselves with demonstrating a easy toy mannequin.
Nonetheless, having seen a easy mannequin in motion, in addition to the kind of knowledge it really works on, ought to assist lots in understanding how
DL can be utilized for climate prediction.
Dataset
Weatherbench was explicitly created as a benchmark dataset and thus, as is
frequent for this species, hides a number of preprocessing and standardization effort from the person. Atmospheric knowledge can be found
on an hourly foundation, starting from 1979 to 2018, at completely different spatial resolutions. Relying on decision, there are about 15
to twenty measured variables, together with temperature, geopotential, wind pace, and humidity. Of those variables, some are
out there at a number of stress ranges. Thus, our instance makes use of a small subset of obtainable “channels.” To save lots of storage,
community and computational sources, it additionally operates on the smallest out there decision.
This submit is accompanied by executable code on Google
Colaboratory, which shouldn’t simply
render pointless any copy-pasting of code snippets but in addition, permit for uncomplicated modification and experimentation.
To learn in and extract the info, saved as NetCDF information, we use
tidync, a high-level bundle constructed on prime of
ncdf4 and RNetCDF. In any other case,
availability of the standard “TensorFlow household” in addition to a subset of tidyverse packages is assumed.
As already alluded to, our instance makes use of two spatio-temporal collection: 500hPa geopotential and 850hPa temperature. The
following instructions will obtain and unpack the respective units of by-year information, for a spatial decision of 5.625 levels:
download.file("https://dataserv.ub.tum.de/s/m1524895/obtain?path=%2F5.625degpercent2Ftemperature_850&information=temperature_850_5.625deg.zip",
"temperature_850_5.625deg.zip")
unzip("temperature_850_5.625deg.zip", exdir = "temperature_850")
download.file("https://dataserv.ub.tum.de/s/m1524895/obtain?path=%2F5.625degpercent2Fgeopotential_500&information=geopotential_500_5.625deg.zip",
"geopotential_500_5.625deg.zip")
unzip("geopotential_500_5.625deg.zip", exdir = "geopotential_500")Inspecting a kind of information’ contents, we see that its knowledge array is structured alongside three dimensions, longitude (64
completely different values), latitude (32) and time (8760). The information itself is z, the geopotential.
tidync("geopotential_500/geopotential_500hPa_2015_5.625deg.nc") %>% hyper_array()Class: tidync_data (listing of tidync knowledge arrays)
Variables (1): 'z'
Dimension (3): lon,lat,time (64, 32, 8760)
Supply: /[...]/geopotential_500/geopotential_500hPa_2015_5.625deg.ncExtraction of the info array is as simple as telling tidync to learn the primary within the listing of arrays:
[1] 64 32 8760Whereas we delegate additional introduction to tidync to a complete blog
post on the ROpenSci web site, let’s not less than have a look at a fast visualization, for
which we choose the very first time level. (Extraction and visualization code is analogous for 850hPa temperature.)
image(z500_2015[ , , 1],
col = hcl.colors(20, "viridis"), # for temperature, the colour scheme used is YlOrRd
xaxt = 'n',
yaxt = 'n',
fundamental = "500hPa geopotential"
)The maps present how stress and temperature strongly depend upon latitude. Moreover, it’s simple to identify the atmospheric
waves:

Determine 1: Spatial distribution of 500hPa geopotential and 850 hPa temperature for 2015/01/01 0:00h.
For coaching, validation and testing, we select consecutive years: 2015, 2016, and 2017, respectively.
z500_train <- (tidync("geopotential_500/geopotential_500hPa_2015_5.625deg.nc") %>% hyper_array())[[1]]
t850_train <- (tidync("temperature_850/temperature_850hPa_2015_5.625deg.nc") %>% hyper_array())[[1]]
z500_valid <- (tidync("geopotential_500/geopotential_500hPa_2016_5.625deg.nc") %>% hyper_array())[[1]]
t850_valid <- (tidync("temperature_850/temperature_850hPa_2016_5.625deg.nc") %>% hyper_array())[[1]]
z500_test <- (tidync("geopotential_500/geopotential_500hPa_2017_5.625deg.nc") %>% hyper_array())[[1]]
t850_test <- (tidync("temperature_850/temperature_850hPa_2017_5.625deg.nc") %>% hyper_array())[[1]]Since geopotential and temperature will probably be handled as channels, we concatenate the corresponding arrays. To remodel the info
into the format wanted for pictures, a permutation is critical:
[1] 8760 32 64 2All knowledge will probably be standardized in accordance with imply and customary deviation as obtained from the coaching set:
54124.91 274.8In phrases, the imply geopotential peak (see footnote 5 for extra on this time period), as measured at an isobaric floor of 500hPa,
quantities to about 5400 metres, whereas the imply temperature on the 850hPa degree approximates 275 Kelvin (about 2 levels
Celsius).
prepare <- train_all
prepare[, , , 1] <- (prepare[, , , 1] - level_means[1]) / level_sds[1]
prepare[, , , 2] <- (prepare[, , , 2] - level_means[2]) / level_sds[2]
valid_all <- abind::abind(z500_valid, t850_valid, alongside = 4)
valid_all <- aperm(valid_all, perm = c(3, 2, 1, 4))
legitimate <- valid_all
legitimate[, , , 1] <- (legitimate[, , , 1] - level_means[1]) / level_sds[1]
legitimate[, , , 2] <- (legitimate[, , , 2] - level_means[2]) / level_sds[2]
test_all <- abind::abind(z500_test, t850_test, alongside = 4)
test_all <- aperm(test_all, perm = c(3, 2, 1, 4))
take a look at <- test_all
take a look at[, , , 1] <- (take a look at[, , , 1] - level_means[1]) / level_sds[1]
take a look at[, , , 2] <- (take a look at[, , , 2] - level_means[2]) / level_sds[2]We’ll try and predict three days forward.
Now all that continues to be to be completed is assemble the precise datasets.
batch_size <- 32
train_x <- prepare %>%
tensor_slices_dataset() %>%
dataset_take(dim(prepare)[1] - lead_time)
train_y <- prepare %>%
tensor_slices_dataset() %>%
dataset_skip(lead_time)
train_ds <- zip_datasets(train_x, train_y) %>%
dataset_shuffle(buffer_size = dim(prepare)[1] - lead_time) %>%
dataset_batch(batch_size = batch_size, drop_remainder = TRUE)
valid_x <- legitimate %>%
tensor_slices_dataset() %>%
dataset_take(dim(legitimate)[1] - lead_time)
valid_y <- legitimate %>%
tensor_slices_dataset() %>%
dataset_skip(lead_time)
valid_ds <- zip_datasets(valid_x, valid_y) %>%
dataset_batch(batch_size = batch_size, drop_remainder = TRUE)
test_x <- take a look at %>%
tensor_slices_dataset() %>%
dataset_take(dim(take a look at)[1] - lead_time)
test_y <- take a look at %>%
tensor_slices_dataset() %>%
dataset_skip(lead_time)
test_ds <- zip_datasets(test_x, test_y) %>%
dataset_batch(batch_size = batch_size, drop_remainder = TRUE)Let’s proceed to defining the mannequin.
Primary CNN with periodic convolutions
The mannequin is an easy convnet, with one exception: As a substitute of plain convolutions, it makes use of barely extra subtle
ones that “wrap round” longitudinally.
periodic_padding_2d <- operate(pad_width,
title = NULL) {
keras_model_custom(title = title, operate(self) {
self$pad_width <- pad_width
operate (x, masks = NULL) {
x <- if (self$pad_width == 0) {
x
} else {
lon_dim <- dim(x)[3]
pad_width <- tf$forged(self$pad_width, tf$int32)
# wrap round for longitude
tf$concat(list(x[, ,-pad_width:lon_dim,],
x,
x[, , 1:pad_width,]),
axis = 2L) %>%
tf$pad(list(
list(0L, 0L),
# zero-pad for latitude
list(pad_width, pad_width),
list(0L, 0L),
list(0L, 0L)
))
}
}
})
}
periodic_conv_2d <- operate(filters,
kernel_size,
title = NULL) {
keras_model_custom(title = title, operate(self) {
self$padding <- periodic_padding_2d(pad_width = (kernel_size - 1) / 2)
self$conv <-
layer_conv_2d(filters = filters,
kernel_size = kernel_size,
padding = 'legitimate')
operate (x, masks = NULL) {
x %>% self$padding() %>% self$conv()
}
})
}For our functions of creating a deep-learning baseline that’s quick to coach, CNN structure and parameter defaults are
chosen to be easy and reasonable, respectively:
periodic_cnn <- operate(filters = c(64, 64, 64, 64, 2),
kernel_size = c(5, 5, 5, 5, 5),
dropout = rep(0.2, 5),
title = NULL) {
keras_model_custom(title = title, operate(self) {
self$conv1 <-
periodic_conv_2d(filters = filters[1], kernel_size = kernel_size[1])
self$act1 <- layer_activation_leaky_relu()
self$drop1 <- layer_dropout(charge = dropout[1])
self$conv2 <-
periodic_conv_2d(filters = filters[2], kernel_size = kernel_size[2])
self$act2 <- layer_activation_leaky_relu()
self$drop2 <- layer_dropout(charge =dropout[2])
self$conv3 <-
periodic_conv_2d(filters = filters[3], kernel_size = kernel_size[3])
self$act3 <- layer_activation_leaky_relu()
self$drop3 <- layer_dropout(charge = dropout[3])
self$conv4 <-
periodic_conv_2d(filters = filters[4], kernel_size = kernel_size[4])
self$act4 <- layer_activation_leaky_relu()
self$drop4 <- layer_dropout(charge = dropout[4])
self$conv5 <-
periodic_conv_2d(filters = filters[5], kernel_size = kernel_size[5])
operate (x, masks = NULL) {
x %>%
self$conv1() %>%
self$act1() %>%
self$drop1() %>%
self$conv2() %>%
self$act2() %>%
self$drop2() %>%
self$conv3() %>%
self$act3() %>%
self$drop3() %>%
self$conv4() %>%
self$act4() %>%
self$drop4() %>%
self$conv5()
}
})
}
mannequin <- periodic_cnn()Coaching
In that very same spirit of “default-ness,” we prepare with MSE loss and Adam optimizer.
loss <- tf$keras$losses$MeanSquaredError(discount = tf$keras$losses$Discount$SUM)
optimizer <- optimizer_adam()
train_loss <- tf$keras$metrics$Imply(title='train_loss')
valid_loss <- tf$keras$metrics$Imply(title='test_loss')
train_step <- operate(train_batch) {
with (tf$GradientTape() %as% tape, {
predictions <- mannequin(train_batch[[1]])
l <- loss(train_batch[[2]], predictions)
})
gradients <- tape$gradient(l, mannequin$trainable_variables)
optimizer$apply_gradients(purrr::transpose(list(
gradients, mannequin$trainable_variables
)))
train_loss(l)
}
valid_step <- operate(valid_batch) {
predictions <- mannequin(valid_batch[[1]])
l <- loss(valid_batch[[2]], predictions)
valid_loss(l)
}
training_loop <- tf_function(autograph(operate(train_ds, valid_ds, epoch) {
for (train_batch in train_ds) {
train_step(train_batch)
}
for (valid_batch in valid_ds) {
valid_step(valid_batch)
}
tf$print("MSE: prepare: ", train_loss$outcome(), ", validation: ", valid_loss$outcome())
}))Depicted graphically, we see that the mannequin trains nicely, however extrapolation doesn’t surpass a sure threshold (which is
reached early, after coaching for simply two epochs).

Determine 2: MSE per epoch on coaching and validation units.
This isn’t too stunning although, given the mannequin’s architectural simplicity and modest dimension.
Analysis
Right here, we first current two different baselines, which – given a extremely complicated and chaotic system just like the environment – could
sound irritatingly easy and but, be fairly onerous to beat. The metric used for comparability is latitudinally weighted
root-mean-square error. Latitudinal weighting up-weights the decrease latitudes and down-weights the higher ones.
deg2rad <- operate(d) {
(d / 180) * pi
}
lats <- tidync("geopotential_500/geopotential_500hPa_2015_5.625deg.nc")$transforms$lat %>%
select(lat) %>%
pull()
lat_weights <- cos(deg2rad(lats))
lat_weights <- lat_weights / mean(lat_weights)
weighted_rmse <- operate(forecast, ground_truth) {
error <- (forecast - ground_truth) ^ 2
for (i in seq_along(lat_weights)) {
error[, i, ,] <- error[, i, ,] * lat_weights[i]
}
apply(error, 4, imply) %>% sqrt()
}Baseline 1: Weekly climatology
Generally, climatology refers to long-term averages computed over outlined time ranges. Right here, we first calculate weekly
averages based mostly on the coaching set. These averages are then used to forecast the variables in query for the time interval
used as take a look at set.
The first step makes use of tidync, ncmeta, RNetCDF and lubridate to compute weekly averages for 2015, following the ISO
week date system.
train_file <- "geopotential_500/geopotential_500hPa_2015_5.625deg.nc"
times_train <- (tidync(train_file) %>% activate("D2") %>% hyper_array())$time
time_unit_train <- ncmeta::nc_atts(train_file, "time") %>%
tidyr::unnest(cols = c(worth)) %>%
dplyr::filter(title == "models")
time_parts_train <- RNetCDF::utcal.nc(time_unit_train$worth, times_train)
iso_train <- ISOdate(
time_parts_train[, "year"],
time_parts_train[, "month"],
time_parts_train[, "day"],
time_parts_train[, "hour"],
time_parts_train[, "minute"],
time_parts_train[, "second"]
)
isoweeks_train <- map(iso_train, isoweek) %>% unlist()
train_by_week <- apply(train_all, c(2, 3, 4), operate(x) {
tapply(x, isoweeks_train, operate(y) {
mean(y)
})
})
dim(train_by_week)53 32 64 2Step two then runs via the take a look at set, mapping dates to corresponding ISO weeks and associating the weekly averages from the
coaching set:
test_file <- "geopotential_500/geopotential_500hPa_2017_5.625deg.nc"
times_test <- (tidync(test_file) %>% activate("D2") %>% hyper_array())$time
time_unit_test <- ncmeta::nc_atts(test_file, "time") %>%
tidyr::unnest(cols = c(worth)) %>%
dplyr::filter(title == "models")
time_parts_test <- RNetCDF::utcal.nc(time_unit_test$worth, times_test)
iso_test <- ISOdate(
time_parts_test[, "year"],
time_parts_test[, "month"],
time_parts_test[, "day"],
time_parts_test[, "hour"],
time_parts_test[, "minute"],
time_parts_test[, "second"]
)
isoweeks_test <- map(iso_test, isoweek) %>% unlist()
climatology_forecast <- test_all
for (i in 1:dim(climatology_forecast)[1]) {
week <- isoweeks_test[i]
lookup <- train_by_week[week, , , ]
climatology_forecast[i, , ,] <- lookup
}For this baseline, the latitudinally-weighted RMSE quantities to roughly 975 for geopotential and 4 for temperature.
wrmse <- weighted_rmse(climatology_forecast, test_all)
round(wrmse, 2)974.50 4.09Baseline 2: Persistence forecast
The second baseline generally used makes an easy assumption: Tomorrow’s climate is at present’s climate, or, in our case:
In three days, issues will probably be identical to they’re now.
Computation for this metric is nearly a one-liner. And because it seems, for the given lead time (three days), efficiency is
not too dissimilar from obtained by the use of weekly climatology:
937.55 4.31Baseline 3: Easy convnet
How does the straightforward deep studying mannequin stack up towards these two?
To reply that query, we first must get hold of predictions on the take a look at set.
test_wrmses <- data.frame()
test_loss <- tf$keras$metrics$Imply(title = 'test_loss')
test_step <- operate(test_batch, batch_index) {
predictions <- mannequin(test_batch[[1]])
l <- loss(test_batch[[2]], predictions)
predictions <- predictions %>% as.array()
predictions[, , , 1] <- predictions[, , , 1] * level_sds[1] + level_means[1]
predictions[, , , 2] <- predictions[, , , 2] * level_sds[2] + level_means[2]
wrmse <- weighted_rmse(predictions, test_all[batch_index:(batch_index + 31), , ,])
test_wrmses <<- test_wrmses %>% bind_rows(c(z = wrmse[1], temp = wrmse[2]))
test_loss(l)
}
test_iterator <- as_iterator(test_ds)
batch_index <- 0
whereas (TRUE) {
test_batch <- test_iterator %>% iter_next()
if (is.null(test_batch))
break
batch_index <- batch_index + 1
test_step(test_batch, as.integer(batch_index))
}
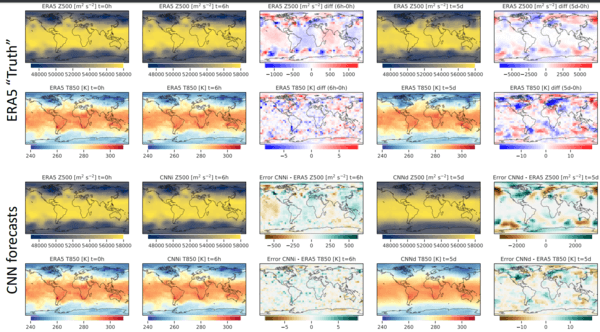
test_loss$outcome() %>% as.numeric()3821.016Thus, common loss on the take a look at set parallels that seen on the validation set. As to latitudinally weighted RMSE, it seems
to be greater for the DL baseline than for the opposite two:
z temp
1521.47 7.70 Conclusion
At first look, seeing the DL baseline carry out worse than the others would possibly really feel anticlimactic. But when you consider it,
there is no such thing as a have to be upset.
For one, given the big complexity of the duty, these heuristics will not be as simple to outsmart. Take persistence: Relying
on lead time – how far into the long run we’re forecasting – the wisest guess may very well be that the whole lot will keep the
identical. What would you guess the climate will appear to be in 5 minutes? — Identical with weekly climatology: Wanting again at how
heat it was, at a given location, that very same week two years in the past, doesn’t basically sound like a nasty technique.
Second, the DL baseline proven is as primary as it might get, architecture- in addition to parameter-wise. Extra subtle and
highly effective architectures have been developed that not simply by far surpass the baselines, however may even compete with bodily
fashions (cf. particularly Rasp and Thuerey (Rasp and Thuerey 2020) already talked about above). Sadly, fashions like that have to be
skilled on lots of information.
Nevertheless, different weather-related functions (aside from medium-range forecasting, that’s) could also be extra in attain for
people within the matter. For these, we hope now we have given a helpful introduction. Thanks for studying!