Suppressing quantum errors by scaling a floor code logical qubit – Google AI Weblog

A few years from immediately, scientists will be capable to use fault-tolerant quantum computer systems for large-scale computations with purposes throughout science and trade. These quantum computer systems will probably be a lot greater than immediately, consisting of hundreds of thousands of coherent quantum bits, or qubits. However there’s a catch — these primary constructing blocks have to be ok or the methods will probably be overrun with errors.

Presently, the error charges of the qubits on our third era Sycamore processor are sometimes between 1 in 10,000 to 1 in 100. By way of our work and that of others, we perceive that growing large-scale quantum computer systems would require far decrease error charges. We’ll want charges within the vary of 1 in 10⁹ to 1 in 10⁶ to run quantum circuits that may resolve industrially related issues.

So how can we get there, realizing that squeezing three to 6 orders of magnitude of higher efficiency from our present bodily qubits is unlikely? Our group has created a roadmap that has directed our analysis for the final a number of years, enhancing the efficiency of our quantum computer systems in gradual steps towards a fault-tolerant quantum laptop.

Roadmap for constructing a helpful error-corrected quantum laptop with key milestones. We’re at present constructing one logical qubit that we’ll scale sooner or later.

Right now, in “Suppressing Quantum Errors by Scaling a Surface Code Logical Qubit”, printed in Nature, we’re saying that we’ve reached the second milestone on our roadmap. Our experimental outcomes exhibit a prototype of the fundamental unit of an error-corrected quantum laptop referred to as a logical qubit, with efficiency nearing the regime that allows scalable fault-tolerant quantum computing.

From bodily qubits to logical qubits

Quantum error correction (QEC) represents a big shift from immediately’s quantum computing, the place every bodily qubit on the processor acts as a unit of computation. It offers the recipe to achieve low errors by buying and selling many good qubits for an wonderful one: data is encoded throughout a number of bodily qubits to assemble a single logical qubit that’s extra resilient and able to operating large-scale quantum algorithms. Underneath the appropriate circumstances, the extra bodily qubits used to construct a logical qubit, the higher that logical qubit turns into.

Nevertheless, this is not going to work if the added errors from every extra bodily qubit outweigh the advantages of QEC. Till now, the excessive bodily error charges have all the time gained out.

To that finish, we use a selected error-correcting code referred to as a floor code and present for the primary time that rising the scale of the code decreases the error fee of the logical qubit. A primary-ever for any quantum computing platform, this was achieved by painstakingly mitigating many error sources as we scaled from 17 to 49 bodily qubits. This work is proof that with sufficient care, we are able to produce the logical qubits mandatory for a large-scale error-corrected quantum laptop.

Quantum error correction with floor codes

How does an error-correcting code defend data? Take a easy instance from classical communication: Bob desires to ship Alice a single bit that reads “1” throughout a loud communication channel. Recognizing that the message is misplaced if the bit flips to “0”, Bob as a substitute sends three bits: “111”. If one erroneously flips, Alice might take a majority vote (a easy error-correcting code) of all of the obtained bits and nonetheless perceive the supposed message. Repeating the data greater than 3 times — rising the “measurement” of the code — would allow the code to tolerate extra particular person errors.

Many bodily qubits on a quantum processor performing as one logical qubit in an error-correcting code referred to as a floor code.

A floor code takes this precept and imagines a sensible quantum implementation. It has to fulfill two extra constraints. First, the floor code should be capable to right not simply bit flips, taking a qubit from |0⟩ to |1⟩, but additionally phase flips. This error is exclusive to quantum states and transforms a qubit in a superposition state, for instance from “|0⟩ + |1⟩” to “|0⟩ – |1⟩”. Second, checking the qubits’ states would destroy their superpositions, so one wants a manner of detecting errors with out measuring the states straight.

To deal with these constraints, we organize two sorts of qubits on a checkerboard. “Knowledge” qubits on the vertices make up the logical qubit, whereas “measure” qubits on the heart of every sq. are used for so-called “stabilizer measurements.” These measurements inform us whether or not the qubits are all the identical, as desired, or completely different, signaling that an error occurred, with out truly revealing the worth of the person knowledge qubits.

We tile two sorts of stabilizer measurements in a checkerboard sample to guard the logical knowledge from bit- and phase-flips. If a few of the stabilizer measurements register an error, then correlations within the stabilizer measurements are used to establish which error(s) occurred and the place.

Floor-code QEC. Knowledge qubits (yellow) are on the vertices of a checkerboard. Measure qubits on the heart of every sq. are used for stabilizer measurements (blue squares). Darkish blue squares verify for bit-flip errors, whereas gentle blue squares verify for phase-flip errors. Left: A phase-flip error. The 2 nearest gentle blue stabilizer measurements register the error (gentle crimson). Proper: A bit-flip error. The 2 nearest darkish blue stabilizer measurements register the error (darkish crimson).

Simply as Bob’s message to Alice within the instance above grew to become extra strong in opposition to errors with rising code measurement, a bigger floor code higher protects the logical data it comprises. The floor code can stand up to quite a lot of bit- and phase-flip errors every equal to lower than half the distance, the place the gap is the variety of knowledge qubits that span the floor code in both dimension.

However right here’s the issue: each particular person bodily qubit is vulnerable to errors, so the extra qubits in a code, the extra alternative for errors. We would like the upper safety supplied by QEC to outweigh the elevated alternatives for errors as we improve the variety of qubits. For this to occur, the bodily qubits should have errors under the so-called “fault-tolerant threshold.” For the floor code, this threshold is sort of low. So low that it hasn’t been experimentally possible till not too long ago. We are actually on the precipice of reaching this coveted regime.

Making and controlling high-quality bodily qubits

Coming into the regime the place QEC improves with scale required enhancing each facet of our quantum computer systems, from nanofabrication of the bodily qubits to the optimized management of the complete quantum system. These experiments ran on a state-of-the-art third era Sycamore processor structure optimized for QEC utilizing the floor code with enhancements throughout the board:

• Elevated qubit rest and dephasing lifetimes via an improved fabrication course of and environmental noise discount close to the quantum processor.
• Lowered cross-talk between all bodily qubits throughout parallel operation by optimizing quantum processor circuit design and nanofabrication.
• Lowered drift and improved qubit management constancy via upgraded customized electronics.
• Applied faster and higher-fidelity readout and reset operations in contrast with earlier generations of the Sycamore processor.
• Lowered calibration errors by extensively modeling the complete quantum system and using higher system-optimization algorithms.
• Developed context-aware and totally parallel calibrations to attenuate drift and optimize management parameters for QEC circuits.
• Enhanced dynamical decoupling protocols to guard bodily qubits from noise and cross-talk throughout idling operations.

Operating floor code circuits

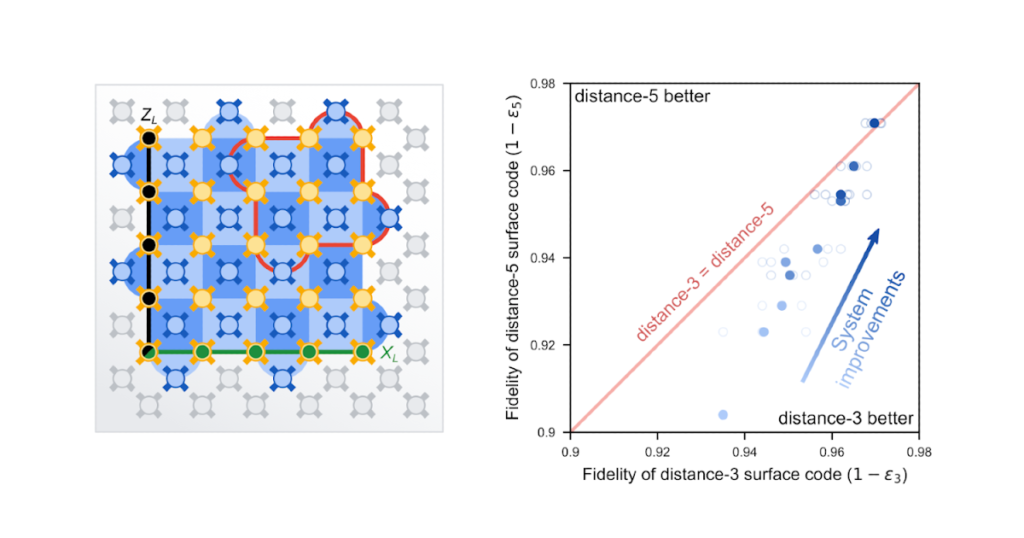
With these upgrades in place, we ran experiments to check the ratio (_3,5) between the logical error fee of a distance-3 floor code (ε₃) with 17 qubits to that of a distance-5 floor code (ε₅) with 49 qubits — _3,5 = ε₃ / ε₅.

Comparability of logical constancy (outlined as 1-ε) between distance-3 (d=3) and distance-5 (d=5) floor codes. The space-5 code comprises 4 attainable distance-3 preparations, with one instance proven within the crimson define (left). As enhancements have been made, the d=5 constancy elevated sooner than that of the d=3, ultimately overtaking the distance-3 code, as proven within the top-right knowledge factors (proper), whose common lies barely to the left of the ε3 = ε5 line.

The outcomes of those experiments are proven above on the appropriate. Continued enhancements over a number of months allowed us to cut back the logical errors of each grids, resulting in the distance-5 grid (ε₅ = 2.914%) outperforming the distance-3 grids (ε₃ = 3.028%) by 4% (_3,5 = 1.04) with 5 confidence. Whereas this would possibly look like a small enchancment, it’s essential to emphasise that the outcome represents a primary for the sector since Peter Shor’s 1995 QEC proposal. A bigger code outperforming a smaller one is a key signature of QEC, and all quantum computing architectures might want to move this hurdle to understand a path to the low errors which can be mandatory for quantum purposes.

The trail ahead

These outcomes point out that we’re coming into a brand new period of sensible QEC. The Google Quantum AI group has spent the previous couple of years interested by how we outline success on this new period, and the way we measure progress alongside the best way.

The last word purpose is to exhibit a pathway to reaching the low errors wanted for utilizing quantum computer systems in significant purposes. To this finish, our goal stays reaching logical error charges of 1 in 10⁶ or decrease per cycle of QEC. Within the determine under on the left, we define the trail that we anticipate to achieve this goal. As we proceed enhancing our bodily qubits (and therefore the efficiency of our logical qubits), we anticipate to progressively improve from near 1 on this work to bigger numbers. The determine under exhibits {that a} worth of = 4 and a code distance of 17 (577 bodily qubits with ok high quality) will yield a logical error fee under our goal of 1 in 10⁶.

Whereas this outcome continues to be a couple of years out, we’ve an experimental method to probe error charges this low with immediately’s {hardware}, albeit in restricted circumstances. Whereas two-dimensional floor codes enable us to right each bit- and phase-flip errors, we are able to additionally assemble one-dimensional repetition codes which can be solely capable of resolve one kind of error with relaxed necessities. On the appropriate under, we present {that a} distance-25 repetition code can attain error charges per cycle near 1 in 10⁶. At such low errors, we see new sorts of error mechanisms that aren’t but observable with our floor codes. By controlling for these error mechanisms, we are able to enhance repetition codes to error charges close to 1 in 10⁷.

Left: Anticipated development as we enhance efficiency (quantified by ) and scale (quantified by code distance) for floor codes. Proper: Experimentally measured logical error charges per cycle versus the gap of one-dimensional repetition codes and two-dimensional floor codes.

Reaching this milestone displays three years of centered work by the complete Google Quantum AI group following our demonstration of a quantum laptop outperforming a classical computer. In our march towards constructing fault-tolerant quantum computer systems, we’ll proceed to make use of the goal error charges within the determine above to measure our progress. With additional enhancements towards our subsequent milestone, we anticipate coming into the fault-tolerant regime, the place we are able to exponentially suppress logical errors and unlock the primary helpful error-corrected quantum purposes. Within the meantime, we proceed to discover varied methods of fixing issues utilizing quantum computer systems in subjects starting from condensed matter physics to chemistry, machine learning, and materials science.